More on random number generators

My previous post described the recent view on random number generators, with a focus on the Mersenne-Twister war.

Since, I have noticed another front in the war of the random number generators:

• An example in dimension 121 from K Savvidy where L’Ecuyer MRG32k3a fails to compute the correct result, regardless of the seed. This is a manufactured example, such that the vector, used in the example, falls in the dual lattice of the generator. Similar examples can be constructed for other variants.
• Spectral Analysis of the MIXMAX Random Number Generator (by L’Ecuyer et al.) shows defects in MIXMAX, for some parameters that were advised in earlier papers of K. Savvidy. MIXMAX is a RNG popularized by K. Savvidy, used in CLHEP at Fermilab.

Also, I found interesting that Monte-Carlo simulations run at the Los Alamos National Laboratory relied on a relatively simple linear congruential generator (LCG) producing 24- or 48-bits integers for at least 40 years. LCGs are today touted as some of the worst random number generators, exhibiting strong patterns in 2D projections. Also the period chosen was very small by today’s standards: 7E13.

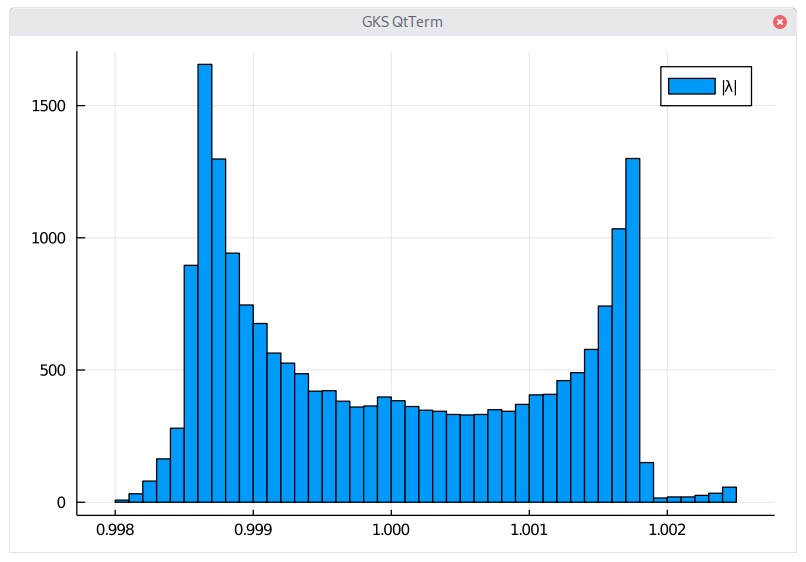
Regarding the integer to floating point numbers conversion, I remember somewhere reading someone arguing to generate numbers also close to 0 (with appropriate distribution) while most implementations just generate up to \(2^{-32}\) or \(2^{-53}\) (the latter being the machine epsilon). I see one major issue with the idea: if you stumble upon a tiny number (perhaps you’re unlucky) like \(10^{-100}\), then it may distort significantly your result (for example if you call the inverse cumulative normal to generate normal numbers and calculate the mean), because your sample size may not be not large enough to compensate. Perhaps for the same kind of reason, it may be better to use only 32 bits (or less bits). The consequence is that tail events are bound to be underestimated by computers. In a way this is similar to Sobol, which generates with a precision of \(2^{-L}\), for \(2^{L} - 1\) samples.

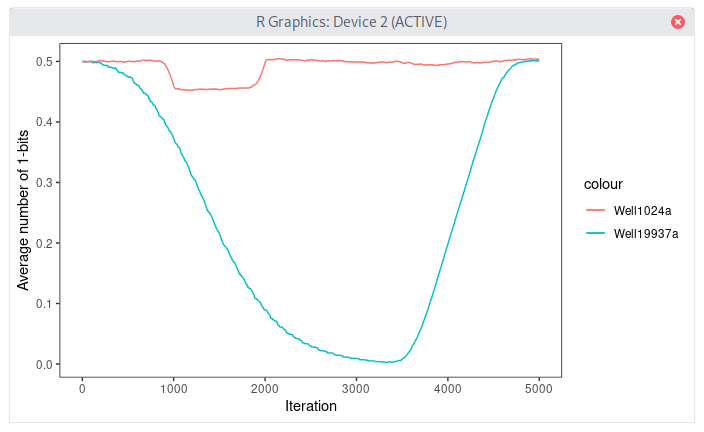
Finally, some personal tests convinced me that a very long period, such as the one in MT, may not be a good idea, as, in the case of MT, the generator is then slower to recover from a bad state. For Well19337a, it may take 5000 numbers and the excess-0 state is very pronounced (period of \(2^{19937}-1\)). While this is way better than the old MersenneTwister (the newer dSFMT is also much better, around twice slower than Well19937a in terms of recovery), which requires more than 700 000 numbers to recover from the bad state, it may still be problematic in some cases. For example, if you are particularly unlucky, and pick a bad choice of initial state (which may actually have good properties in terms of number of 0 bits and 1 bits) and your simulation is of small size (16K o even 64K numbers), there may be visible an impact of this excess-0 state on the simulation results. For Well1024a (period of \(2^{1024}-1\)), full bit balance recovery takes around 500 numbers and the excess-0 state is much much milder so as to be a non-issue really.

Below is an example of (manufactured) bad seed for Well19937a, which will lead to excess-0 state after ~1000 numbers, and lasts ~3000 numbers.

     int[] seed = { 1097019443, 321950666, -1456208324, -695055366, -776027098, 1991742627, 1792927970, 1868278530,
                456439811, 85545192, -1102958393, 1274926688, 876782718, -775511822, 1563069059, 1325885775, 1463966395,
                2088490152, 382793542, -2132079651, 1612448076, -1831549496, 1925428027, 2056711268, 108350926,
                1369323267, 149925491, 1803650776, 614382824, 2065025020, 1307415488, -535412012, -1628604277,
                1678678293, -516020113, -1021845340, -793066208, -802524305, -921860953, -1163555006, -1922239490,
                1767557906, -759319941, -245934768, 939732201, -455619338, 1110635951, -86428700, 1534787893,
                -283404203, 227231030, -313408533, 556636489, -673801666, 710168442, 870157845, 1109322330, -1059935576,
                -513162043, 1192536003, -1602508674, 1246446862, 1913473951, 1960859271, 782284340, 122481381,
                -562235323, 202010478, -221077141, -1910492242, -138670306, -2038651468, 664298925, -156597975,
                -48624791, 1658298950, 802966298, -85599391, -406693042, 1340575258, 1456716829, -1747179769,
                1499970781, 1626803166, -687792918, -1283063527, 733224784, 193833403, -230689121, 775703471, 808035556,
                337484408, -518187168, -2136806959, -2115195080, -2137532162, 873637610, 216187601, -477469664,
                -1324444679, 1339595692, 378607523, 2100214039, 701299050, -178243691, 1858430939, 1595015688,
                2139167840, 500034546, -1316251830, 1619225544, 1075598309, 1300570196, -327879940, 414752857,
                -145852840, -1287095704, 355046097, 886719800, -20251033, 1202484569, -96793140, 1846043325, 1192691985,
                928549445, 2049152139, -1431689398, 348315869, -1582112142, -1867019110, 808920631, -342499619,
                -1714951676, 279967346, 385626112, 416794895, -578394455, -1827493006, -2020649044, -396940876,
                937037281, -385129309, -1905687689, -526697401, -1362989274, 1111153207, 27104439, 115923124,
                -1759234934, 495392989, 1848408810, 655641704, 1484391560, 128171526, -91609018, 647891731, 1451120112,
                882107541, 1391795234, -1635408453, 936540423, 564583769, 379407298, -1829214977, 1416544842, 81232193,
                -936231221, 1193495035, 1076101894, 860381190, 728390389, -511922164, -1588243268, -142612440,
                1018644290, 292363137, 475075683, -2071023028, -1224051451, -891502122, 1575411974, -123928662,
                1080946339, 962151951, -1309758596, -558497752, -2126110624, -73575762, -2078269964, -676979806,
                -1165971705, 557833742, -828399554, -1023609625, -482198028, 1700021748, 25284256, -826748852,
                -2139877059, -1280388862, -1521749976, 738911852, -1676794665, -1595369910, -748407377, -709662760,
                680897802, 2094081, -1889225549, -1101409768, -1620191266, 506408464, 1833777989, 244154307,
                -1406840497, -860371799, 1337820797, 614831742, 1965416365, 2044401180, -459642558, -339576217,
                -1599807697, -689958382, 1544444702, 872938368, 871179645, -957732397, 958439335, -770544793,
                -1363785888, -1484683703, 2021823060, -1871739595, -1355536561, -926333946, -1552155978, -171673777,
                993986110, -727417527, 1065139863, 517970706, -453434939, -424362471, 1823459056, -48408572, 863024600,
                190046576, 90264753, 1667010014, -529079929, -1269908431, -2073435303, -1123302722, -1986096205,
                -173411290, -693808986, -1618071944, 990740121, 2120678917, -203702980, -1186456799, -776433190,
                172239859, 126482680, 2048550654, 266718714, 913094204, -937686511, -2096719726, 627687384, 533376951,
                -1413352057, 1900628390, -244457985, 896712029, -1232645079, 1109406070, 1857772786, 86662738,
                -488754308, 360849611, 1187200060, -341213227, 1705204161, -121052077, 1122608367, 2118749875,
                243072462, 204425155, 1386222650, 2037519370, 93424131, -785650065, 45913153, -448515509, -1312863705,
                -834086187, -2101474931, 1478985081, 1288703145, -1705562554, -1758416930, 1440392126, 1783362885,
                279032867, -610479214, 223124643, -367215836, 2140908029, -780932174, 581404379, -1741002899,
                2035577655, -1060511248, 1765488586, -380048770, 1175692479, -1645645388, 1865881815, 2052353285,
                -492798850, -1250604575, -2077294162, 1768141964, 1457680051, -141958370, -1333097647, -285257998,
                -2063867587, 1338868565, -304572592, -1272025276, 1687010269, -1301492878, -931017010, -1303123181,
                -1963883357, 1920647644, 2009096326, 2094563567, 1137063943, -1003295201, -382759268, 1879016739,
                -153929025, -1008981939, -646846913, 1209637755, 1560292706, 725377476, -1457854811, 264360697,
                -197926409, -908579207, -894726681, 194950082, -1631939812, 1620763228, -659722026, 208285727,
                1389336301, -1900616308, 1690406628, 1688632068, -717888847, -1202067733, -2039964596, 1885630763,
                475497380, -488949843, -1679189364, -1358405375, 2132723, -1164703873, -1727721852, 1747612544,
                -885752188, -1450470713, 791640674, 996275741, 397386006, -1977069145, -1841011156, -431458913,
                47865163, 1200765705, 1962743423, 1933688124, -1165500082, -1969953200, 597796878, 1379082884,
                -737292673, 1776141019, 1882257528, -991388501, -1357999809, 497686068, 314237824, -882469634,
                2142408833, -1624234776, -292985482, -412114618, 380982413, -1351123340, 1799246791, 491394003,
                496521378, 1074735076, 1131599274, -1379708840, -256028322, 118705543, 58715272, -449189848, 35299724,
                -1440805390, -893785929, 217256482, 640658194, -1786418454, 1111743603, -2027083091, 2022760758,
                -1001437881, -202791246, 636755388, 1243592208, 1858140407, 1909306942, 1350401794, 188044116,
                1740393120, -2013242769, 207311671, 1861876658, -962016288, -865105271, -15675046, -1273011788, 9226838,
                906253170, -1561651292, -300491515, -409022139, 611623625, 1529503331, 943193131, -1180448561, 88712879,
                1630557185, -17136268, -1208615326, 428239158, 256807260, -918201512, 2022301052, -1365374556,
                -877812100, 2029921285, -1949144213, 2053000545, -563019122, 224422509, 741141734, -1881066890,
                -280201419, 1959981692, 302762817, 477313942, 358330821, -1944532523, -980437107, -1520441951,
                -613267979, -1540746690, -1180123782, -1604767026, 1407644227, -926603589, 1418723393, 2045743273,
                -309117167, 949946922, -105868551, -487483019, 1715251004, -221593655, 2116115055, -1676820052,
                394918360, -2111378352, 1723004967, -224939951, -730823623, -200901038, -2133041681, 1627616686,
                -637758336, -1423029387, 1400407571, 861573924, 1521965068, -614045374, 412378545, 2056842579,
                -225546161, 1660341981, 1707828405, -513776239, -115981255, -1996145379, -2009573356, 44694054,
                616913659, 1268484348, -980797111, -464314672, 1545467677, 174095876, -1260470858, 1508450002,
                1730695676, -613360716, 2086321364, -144957473, 202989102, 54793305, -1011767525, 2017450362,
                -761618523, 1572980186, -138358580, 1111304359, 1367056877, 1231098679, 2088262724, 1767697297,
                -921727838, 1743091870, 974339502, 1512597341, -1908845304, 1632152668, -987957372, 1394083911,
                433477830, 579364091, -27455347, -772772319, -478108249, 641973067, -1629332352, 1599105133, 1191519125,
                862581799, -850973024, -188136014, -398642147, 513836556, 1899961764, 2110036944, 512068782,
                -1988800041, -2054857386, 321551840, -1717823978, -1311127543, 373759091, 71650043, 565005405,
                1033674609, 1344695234, 709315126, 1711256293, -1226183001, -1451283945, 628494029, 1635747262,
                -689919247, 1091991202, 1283978365, 749078685, 1987661236, 1992010052, -2003794364, 2099683431,
                267011343, -1326783466, 678839392, -312043613, 1565061780, 178873340, -719911279, -314555472,
                -231514590, 161027711, 1080368165, 1660461722, -337050383, 399572447, -1555785489, -1502682588,
                2143158964, 592925741, -980213649, -724779906, 395465301, 635561967, 700445106, 1198493979, 1707436053,
                149364933, -1767142986, 1950272542, -819076405, 687992680, 1960992977, 1342528780, -2110840904,
                340172712, -486861654 };

The war of the random number generators

These days, there seems to be some sort of small war to define what is a modern good random number generators to advise for simulations. Historically, the Mersenne-Twister (MT thereafter) won this war. It is used by default in many scientific libraries and software, even if there has been a few issues with it:

1. A bad initial seed may make it generate a sequence of low quality for at least as many as 700K numbers.
2. It is slow to jump-ahead, making parallelization not so practical.
3. It fails some TestU01 Bigcrush tests, mostly related to the F2 linear algebra, the algebra of the Mersenne-Twister.

It turns out, that before MT (1997), a lot of the alternatives were much worse, except, perhaps, RANLUX (1993), which is quite slow due to the need of skipping many points of the generated sequence.

The first issue has been mostly solved by more modern variants such as MT-64 or Well19937a or Memt19997. The warm-up needed has been thus significantly shortened, and a better seed initialization is present in those algorithms. It is not clear however that it has been fully solved, as there are very few studies analyzing the quality with many different seeds, I found only a summary of one test, p.7 of this presentation.

The second issue may be partly solved by considering a shorter period, such as in the Well1024 generator.

The third issue may or may not be a real issue in practice. Those tests can be seen as taylored to make MT (and F2 algebra based generators) fail and not be all that practical. However, Vigna exposes the problem on some more concrete examples in his recent paper. The title of this paper has the provocative title It Is High Time We Let Go Of The Mersenne Twister. Before that paper, Vigna and her arch-enemy O’Neil, regularly advised to let go of the Mersenne-Twister and use a generator they created instead. For Vigna, the generator is some variant of xorshift, the most recent being xoroshiro256**, and for O’Neil, it is one of her numerous PCG algorithms. In both cases, a flurry of generators is proposed, and it seems that a lot of them are poor (Vigna criticizes strongly PCG on his personal page; O’Neil does something similar against xorshift variants sometimes with the help of Lemire). The recommended choice for each has evolved over the years. For a reader or a user, it looks then that both are risky/unproven. The authors of MT recently also added their own opinion on a specific xorshift variant (xorshift128+), with their papers Again, random numbers fall mainly in the planes: xorshift128+ generators and Pseudo random number generators: attention for a newly proposed generator. An important insight of that latter paper, is to insist that it is not enough to pass a good test suite like BigCrush for a generator to be good.

So what is recommended then?

A good read on the subject is another paper, with the title Pseudorandom Number Generation: Impossibility and Compromise, also from the MT authors, explaining the challenge of defining what is a good random number generator. It ignores however the MRG family of generator studied by L’Ecuyer, whose MRG32k3a is also relatively widely used, and has been there for a while now without any obvious defect against it being proven (good track record). This generator has a relatively fast jump-ahead, which is one of the reasons why it regained popularity with the advent of GPUs and does not fail TestU01 BigCrush. It is a bit slower than MT, but not much, especially with this implementation from Vigna (3x faster than original double based implementation).

There are not many studies on block based crypto-generator such as AES or Chacha for simulation, which become a bit more trendy (thanks to Salmons paper) as they are trivial use in a parallel Monte-Carlo simulation (jump-ahead as fast as generation of one number). In theory the uniformity should be good, since otherwise that would be a channel of attack.

The conclusion of the presentation referenced earlier in this post, is also very relevant:

• use the best sequential generators (i.e. MT, MRG32k3a or some Well),
• test the stochastic variability by changing generator,
• do not parallelize by inputing different seeds (prefer a jump-ahead or a tested substream approach).

Sobol with 64-bits integers

A while ago, I wondered how to make some implementation of Sobol support 64-bits integers (long) and double floating points. Sobol is the most used quasi random number generator (QRNG) for (quasi) Monte-Carlo simulations.

The standard Sobol algorithms are all coded with 32-bits integers and lead to double floating point numbers which can not be smaller than \( 2^{-31} \). I was recently looking back at the internals at Sobol generators, and noticed that generating with 64-bits integers would not help much.

A key to understanding why is to analyze exactly what is the output that Sobol generates. If one asks for a sequence of N numbers (in dimension D), the output will be a multiple of \( 2^{-L} \) where L is the log-2 of N. The 32 bits only become useful when \( N > 2^{31} \). An implementation with 64-bit integers becomes only useful if we query an extremely long sequence (longer than 1 billion numbers), which is not all that practical in reality. Furthermore, the direction numbers would then require double the amount of memory (which may be relatively large for 20K dimensions).

Another interesting detail I learnt recently was to avoid skipping the first point, when scrambling (or randomization) is applied, as per this article from Owen (2020). In a non-randomized or non-scrambled setting, we skip the first point typically because it is 0, and 0 is often problematic, for example if we need to take the inverse cumulative distribution function, to simulate a specific distribution. What I find slightly surprising is that there is no symmetry between 1 and 0: the point (1, 1) is never generated by a two-dimensional Sobol generator, but (0, 0) is the first number. If we apply some sort of inverse cumulative distribution (and no scrambling), it looks like then the result would be skewed towards negative infinity.

Intel failure and the future of computing

What has been happening to the INTC stock today may be revealing of the future. The stock dropped more than 16%, mainly because they announced that their 7nm process does not work (well) and they may rely on an external foundry for their processors. Initially, in 2015, they thought they would have 8nm process by 2017, and 7nm by 2018. They are more than 3 years late.

Intel used to be a leader in the manufacturing process for microprocessor. While the company has its share of internal problems, it may also be that we are starting to hit the barrier, where it becomes very difficult to improve on the existing. The end of Moore’s law has been announced many times, it was already a subject 20 years ago. Today, it may be real, if there is only a single company capable of manufacturing processor using a 5nm process (TSMC).

It will be interesting to see what this means for software in general. I suppose clever optimizations and good parallelization may start playing a much more important role. Perhaps we will see also more enthusiasm towards specialized processors, somewhat similar to GPUs and neural network processors.

March 9, 2020 crash - where will CAC40 go?

The stock market crashed by more than 7% on March 9, 2020. It is one of the most important drop since September 2001. I looked at BNP warrant prices on the CAC40 French index, with a maturity of March 20, 2020 , to see what they would tell about the market direction on the day of the crash. This is really a not-so-scientific experiment.

The quotes I got were quite noisy. I applied a few different techniques to imply the probability density from the option prices:

• The one-step Andreasen-Huge with some regularization. The regularization is a bit too mild, although, in terms of implied vol, this was the worst fit among the techniques.
• The stochastic collocation towards a septic polynomial, no regularization needed here. The error in implied volatilities is similar to Andreasen-Huge, even though the implied density is much smoother. I however discovered a small issue with the default optimal monotonic fit, and had to tweak a little bit the optimal polynomial, more on this later in this post.
• Some RBF collocation of the implied vols. Best fit, with regularization, and very smooth density, which however becomes negative in the high strikes.
• Some experimental Andreasen-Huge like technique, with a minimal grid and good regularization.

The implied forward price was around 4745.5. Interestingly, this corresponds to the first small peak visible on the blue and red plots. The strongest peak is located a little beyond 5000, which could mean that the market believes that the index will go back up above 5000. This does not mean that you should buy however, as there are other, more complex explanations. For example, the peak could be a latent phenomenon related to the previous days.

Now here is how the plot is with the “raw” optimal collocation polynomial:

Notice the spurious peak. In terms of implied volatility, this corresponds to a strange, unnatural angle in the smile. The reason for this unnatural peak lies in the details of the stochastic collocation technique: the polynomial we fit is monotonic, but ends up with slope close to zero at some point in order to better fit the data. If the slope is exactly zero, there is a discontinuity in the density. Here the very low slope tranlates to the peak. The fix is simply to impose a floor on the slope (although it may not be obvious in advance to know how much this floor should be).

And for the curious, here are the implied vol plots:

42

Today my 6-years old son came with a math homework. The stated goal was to learn the different ways to make 10 out of smaller numbers. I was impressed. Immediately, I wondered

how many ways are there to make 10 out of smaller numbers?

This is one of the beauties of maths: a very simple problem, which a 6-years old can understand, may actually be quite fundamental. If you want to solve this in the general case, for any number instead of 10, you end up with the partition function. And in order to find this, you will probably learn recurrence relations. So what is the answer for 10?

42

Then I looked at one exercise they did in class, which was simply to find different ways to pay 10 euros with bills of 10, 5 and coins of 2 and 1 euro(s).

Numba, Pypy Overrated?

Many benchmarks show impressive performance gains with the use of Numba or Pypy. Numba allows to compile just-in-time some specific methods, while Pypy takes the approach of compiling/optimizing the full python program: you use it just like the standard python runtime. From those benchmarks, I imagined that those tools would improve my 2D Heston PDE solver performance easily. The initialization part of my program contains embedded for loops over several 10Ks elements. To my surprise, numba did not improve anything (and I had to isolate the code, as it would not work on 2D numpy arrays manipulations that are vectorized). I surmise it does not play well with scipy sparse matrices. Pypy did not behave better, the solver became actually slower than with the standard python interpreter, up to twice as slow, for example, in the case of the main solver loop which only does matrix multiplications and LU solves sparse systems. I did not necessarily expect any performance improvement in this specific loop, since it only consists in a few calls to expensive scipy calculations. But I did not expect a 2x performance drop either.

While I am sure that there are good use cases, especially for numba, I was a bit disappointed that it likely would require to significantly change my code to have any effect (possibly to not do the initialization with scipy sparse matrices, but then, it is not so clear how). Also, I find most benchmarks dumb. For example, the 2D ODE solver of the latter uses a simple dense 2D numpy array. On real code, things are not as simple.

Next I should try Julia again out of curiosity. I tried it several years ago in the context of a simple Monte-Carlo simulation and my experiment at the time was not all that encouraging, but it may be much better at building PDE solvers and not too much work to port my python code. I am curious to see if it ends up being faster, and whether the accessible LU solvers are any good. If Julia delivers, it’s a bit of a shame for python, since it has so many excellent high quality numerical libraries. Also when I look back at my old Monte-Carlo test, I bet it would benefit greatly from numba, somewhat paradoxically, compared to my current experiment.

About

I just moved my blog to a static website, created with Hugo, I explain the reasons why here. You can find more about me on my linkedin profile. In addition you might find the following interesting:

• List of quantitative finance papers I have freely available on SSRN
• TR-BDF2 for Stable American Option Pricing. This is the first draft, not the final version that was published in the Journal of Computational Finance.
• Presentation on finite difference techniques for arbitrage-free SABR I gave at the conference on models and numerics in financial mathematics at the Lorentz center in 2015.
• Exact Forward for Finite-Difference Schemes on the Log-transformed Black-Scholes PDE.
• Asymptotic bounds of the normal volatility.

Fixing NaNs in Quadprog

Out of curiosity, I tried quadprog as open-source quadratic programming convex optimizer, as it is looks fast, and the code stays relatively simple. I however stumbled on cases where the algorithm would return NaNs even though my inputs seemed straighforward. Other libraries such as CVXOPT did not have any issues with those inputs.

Searching on the web, I found that I was not the only one to stumble on this kind of issue with quadprog. In particular, in 2014, Benjamen Tyner gave a simple example in R, where solve.QP returns NaNs while the input is very simple: an identity matrix with small perturbations out of the diagonal. Here is a copy of his example:

    library(quadprog)

    n <- 66L

    set.seed(6860)
    X <- matrix(1e-20, n, n)
    diag(X) <- 1
    Dmat <- crossprod(X)
    y <- seq_len(n)
    dvec <- crossprod(X, y)

    Amat <- diag(n)
    bvec <- y + runif(n)

    sol <- solve.QP(Dmat, dvec, Amat, bvec, meq = n)

    print(sol$solution) # this gives all NaNs

Other people stumbled on similar issues.

In my specific case, I was able to debug the quadprog algorithm and find the root cause: two variables \(g_c\) and \(g_s\) can become very small, and their square becomes essentially zero, creating a division by zero. If, instead of computing \( \frac{g_s^2}{g_c^2} \) we compute \( \left(\frac{g_s}{g_c}\right)^2 \), then the division by zero is avoided as the two variables are of the same order.

While it probably does not catter for all the possible NaN use cases, it did fix all the cases I stumbled upon.

On the Probability of a Netflix Stock Crash

This is a follow up to my previous post where I explore the probability of a TSLA stock crash, reproducing the results of Timothy Klassen.

According to the implied cumulative probability density, TSLA has around 15% chance of crashing below $100. Is this really high compared to other stocks? or is it the interpretation of the data erroneous?

Here I take a look at NFLX (Netflix). Below is the implied volatility according to three different models.

Again, the shape is not too difficult to fit, and all models give nearly the same fit, within the bid-ask spread as long as we include an inverse relative bid-ask spread weighting in the calibration.

The corresponding implied cumulative density is

More explicitely, we obtain

The probability of NFLX moving below $130 is significantly smaller than the probability of TSLA moving below $100 (which is also around the same 1/3 of the spot price).

For completeness, the implied probability density is

I did not particularly optimize the regularization constant here. The lognormal mixture can have a tendency to produce too large bumps in the density at specific strikes, suggesting that it could also benefit of some regularization.

What about risky stocks like SNAP (Snapchat)? It is more challenging to imply the density for SNAP as there are much fewer traded options on the NASDAQ: less strikes, and a lower volume. Below is an attempt.

We find a probability of moving below 1/3 of the current price lower than with TSLA: around 12% SNAP vs 15% for TSLA.