On the Probability of a Netflix Stock Crash
This is a follow up to my previous post where I explore the probability of a TSLA stock crash, reproducing the results of Timothy Klassen.
According to the implied cumulative probability density, TSLA has around 15% chance of crashing below $100. Is this really high compared to other stocks? or is it the interpretation of the data erroneous?
Here I take a look at NFLX (Netflix). Below is the implied volatility according to three different models.
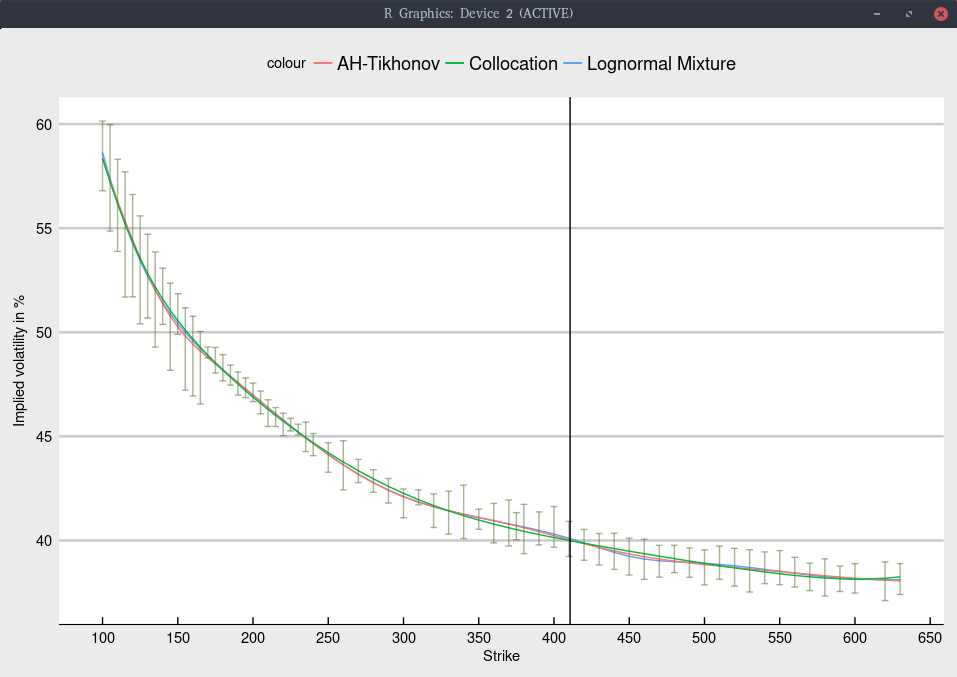
Black volatility implied from Jan 2020 NFLX options.
Again, the shape is not too difficult to fit, and all models give nearly the same fit, within the bid-ask spread as long as we include an inverse relative bid-ask spread weighting in the calibration.
The corresponding implied cumulative density is
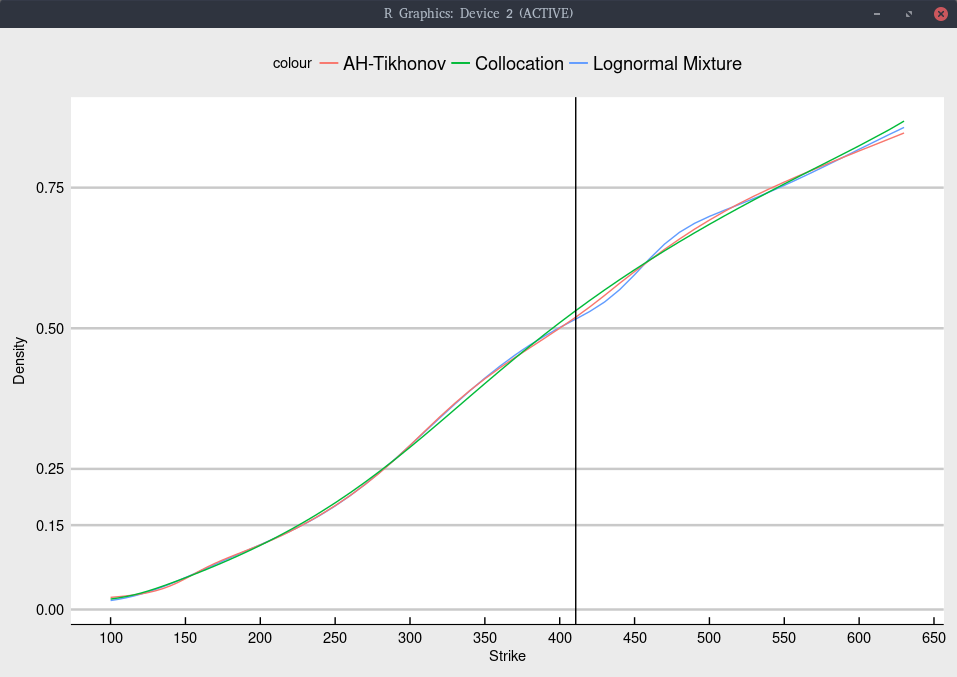
Cumulative density implied from Jan 2020 NFLX options.
More explicitely, we obtain
| Model | probability of NFLX < 130 |
|---|---|
| Collocation | 3.3% |
| Lognormal Mixture | 3.6% |
| Andreasen-Huge regularized | 3.7% |
The probability of NFLX moving below $130 is significantly smaller than the probability of TSLA moving below $100 (which is also around the same 1/3 of the spot price).
For completeness, the implied probability density is
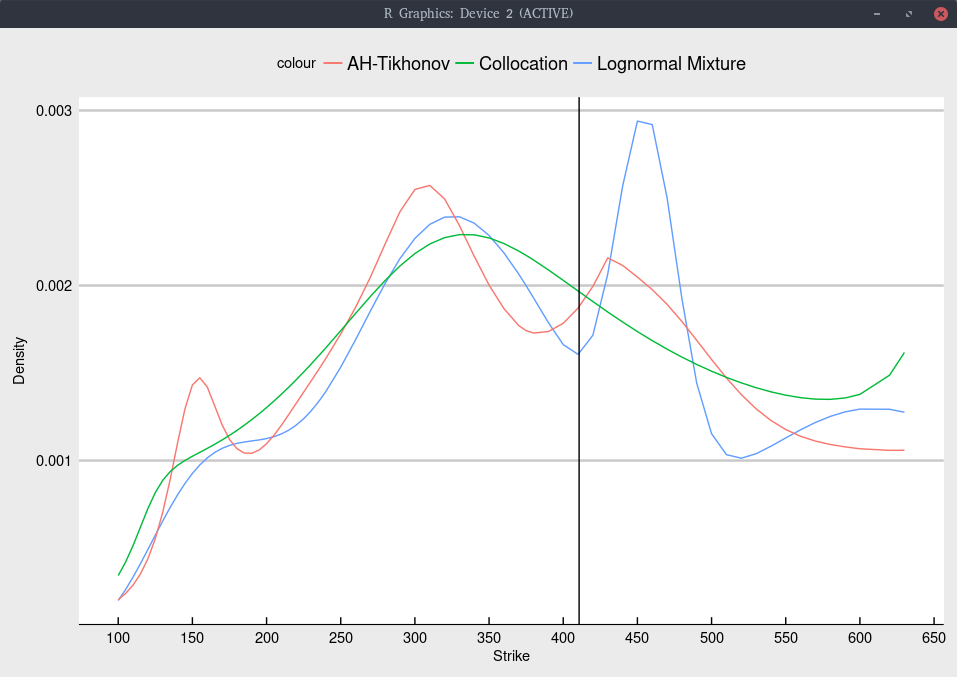
Probability density implied from Jan 2020 NFLX options.
I did not particularly optimize the regularization constant here. The lognormal mixture can have a tendency to produce too large bumps in the density at specific strikes, suggesting that it could also benefit of some regularization.
What about risky stocks like SNAP (Snapchat)? It is more challenging to imply the density for SNAP as there are much fewer traded options on the NASDAQ: less strikes, and a lower volume. Below is an attempt.
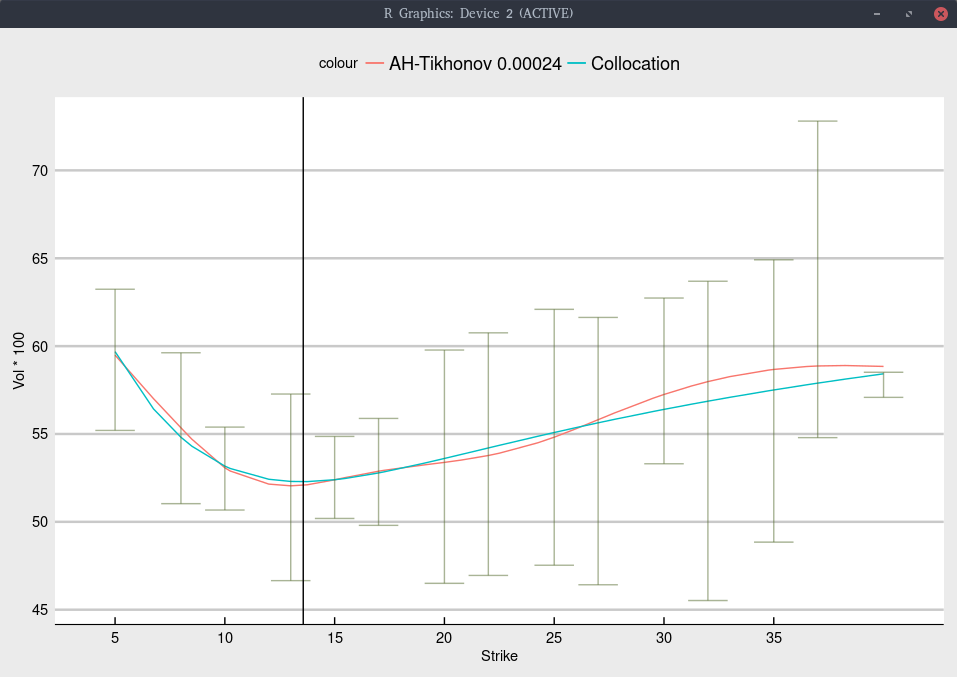
Black volatility implied from Jan 2020 SNAP options.
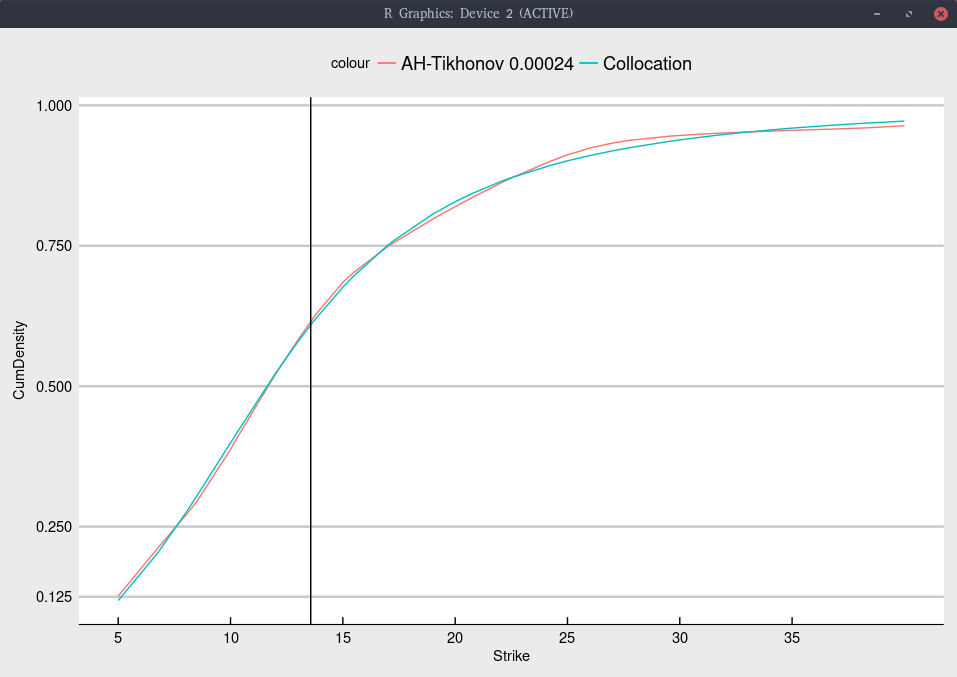
Cumulative density implied from Jan 2020 SNAP options.
We find a probability of moving below 1/3 of the current price lower than with TSLA: around 12% SNAP vs 15% for TSLA.