A new scheme for Heston
I stumbled recently upon a new Heston discretisation scheme, in the spirit of Alfonsi, not more complex and more accurate.
My first attempt at coding the scheme resulted in a miserable failure even though the described algorithm looked not too difficult. I started wondering if the paper, from a little known Lithuanian mathematical journal, was any good. Still, the math in it is very well written, with a great emphasis on the settings for each proposition.
I decided to simply send an email to Prof. Mackevicius, and got a reply the next day (the internet is wonderful sometimes). The exchange helped me to find out that the error was not where I was looking. After spending a bit more time on the paper, I discovered there was simply a missing step in the algorithm.
In between step 3 and step 4, we should have $$ \bar{x} = \frac{\bar{x}\sigma - \bar{y}\rho}{\sigma^2 \sqrt{1-\rho^2}}$$ $$ \bar{y} = \frac{\bar{y}}{\sigma^2}$$
corresponding to the transformation between equations 4.2 and 4.3 of the 2015 paper.
With the added step, the scheme works well. Even if there is clearly an effort from the authors to make their
very mathematically detailed paper more practical with a description of an algorithm, it looks like I have been the first person
to actually try it.
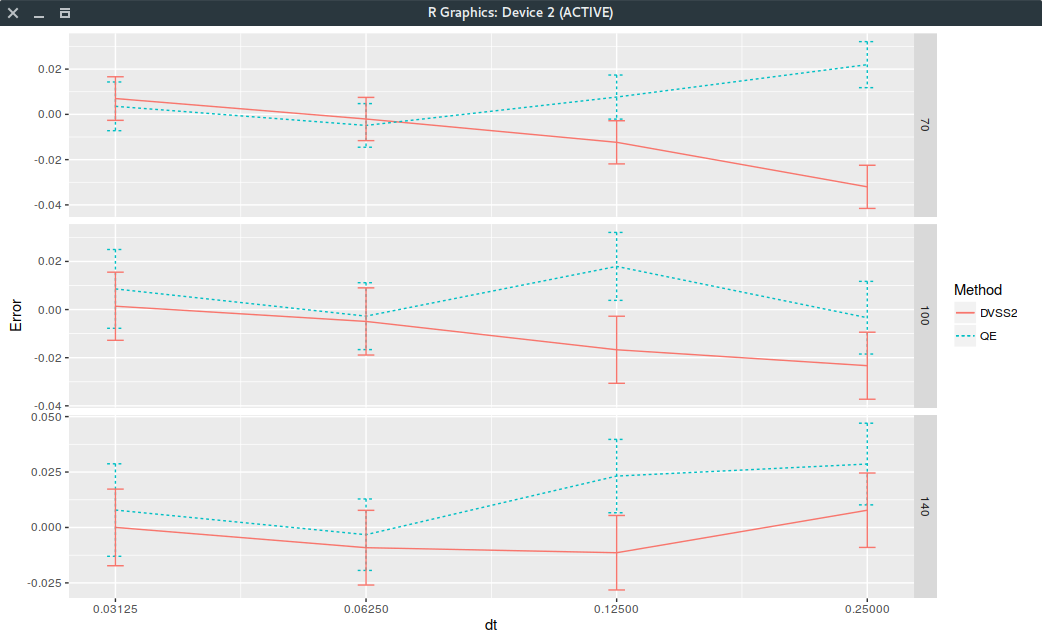
Error on Leif Andersen Case III.
Update January 23rd The scheme does not behave very well on Vanilla forward start options.