Monotonicity of the Black-Scholes Option Prices in Practice

It is well known that vanilla option prices must increase when we increase the implied volatility. Recently, a post on the Wilmott forums wondered about the true accuracy of Peter Jaeckel implied volatility solver, whether it was truely IEEE 754 compliant. In fact, the author noticed some inaccuracy in the option price itself. Unfortunately I can not reply to the forum, its login process does not seem to be working anymore, and so I am left to blog about it.

It can be quite challenging to evaluate the accuracy. For example, one potential error that the author makes is to use numbers that are not exactly representable in IEEE 754 standard such as 4.45 or 0.04. In Julia, and I believe in Python mpmath as well, there is a difference between a BigFloat(4.45) and a BigFloat(“4.45”):

BigFloat(4.45) = 4.45000000000000017763568394002504646778106689453125 BigFloat("4.45")= 4.449999999999999999999999999999999999999999999999999999999999999999999999999972

If we work only on usual 64-bit floats, we likely want to estimate the accuracy of an implementation using BigFloat(4.45) as input rather than BigFloat(“4.45”). To compute a vanilla option price, the naive way would be through the cumulative normal distribution function (the textbook way), which looks like

function bs(strike, forward, voltte)
    d1 = (log(forward/strike)+voltte^2 / 2)/voltte
    return forward*cdf(Normal(),d1)-strike*cdf(Normal(),d1-voltte)
end

It turns out that this produces relatively high error for out of the money prices. In fact, the prices are far from being monotonic if we increase the vol by 1 ulp a hundred times we obtain:

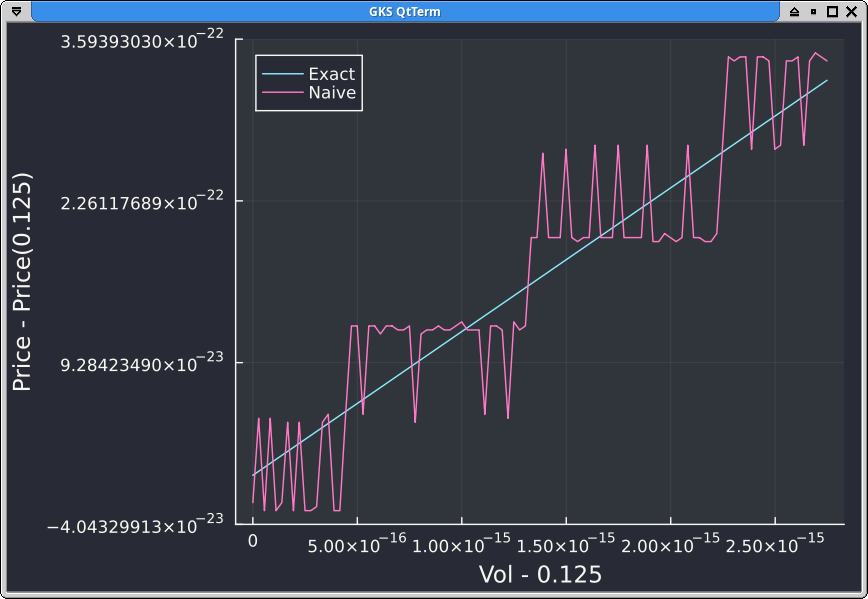
Peter Jaeckel proposes several improvements, the first simple one is to use the scaled complementary error function erfcx rather than the cumulative normal distribution function directly. A second improvement is to use Taylor expansions for small prices. It turns out that on the example with strike K=2.0, forward F=1.0, vol=0.125, the Taylor expansion is being used.

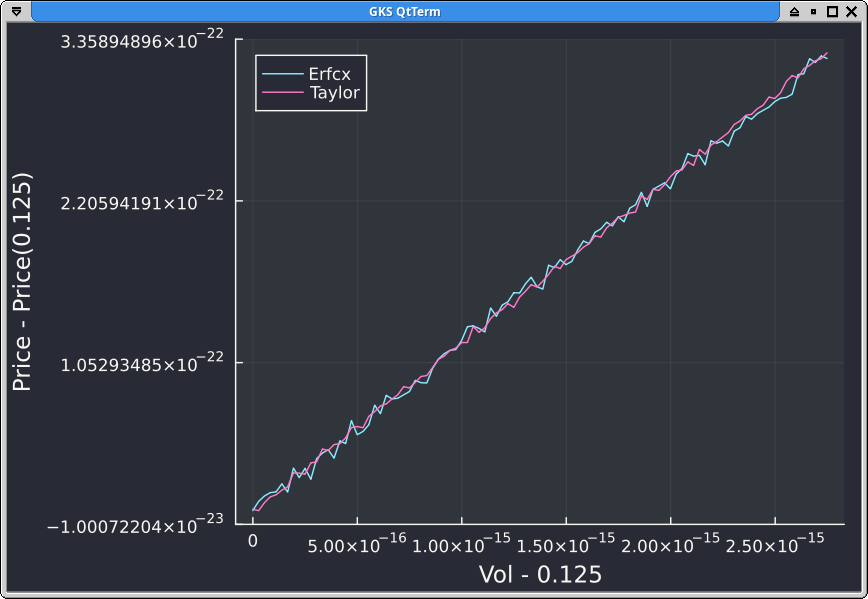
The error is much lower, with Taylor being even a little bit better. But the price is still not monotonic.

How would the implied vol corresponding to those prices look like? If we apply Peter Jaeckel implied vol solver to the naive Black-Scholes formula, we end up with an accuracy limited by the naive formula.

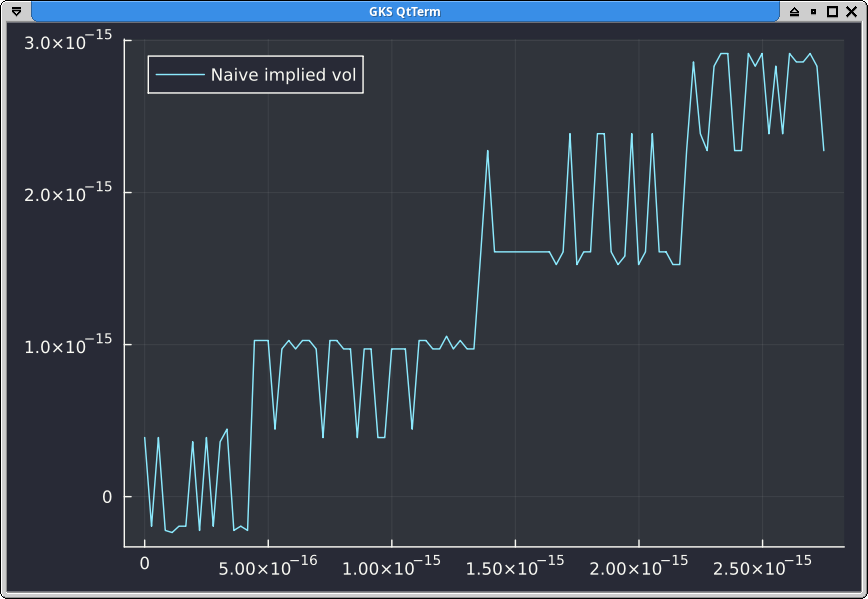
If we apply it to the exact prices or to erfcx or to Taylor, we still end up with a non monotonic implied vol:

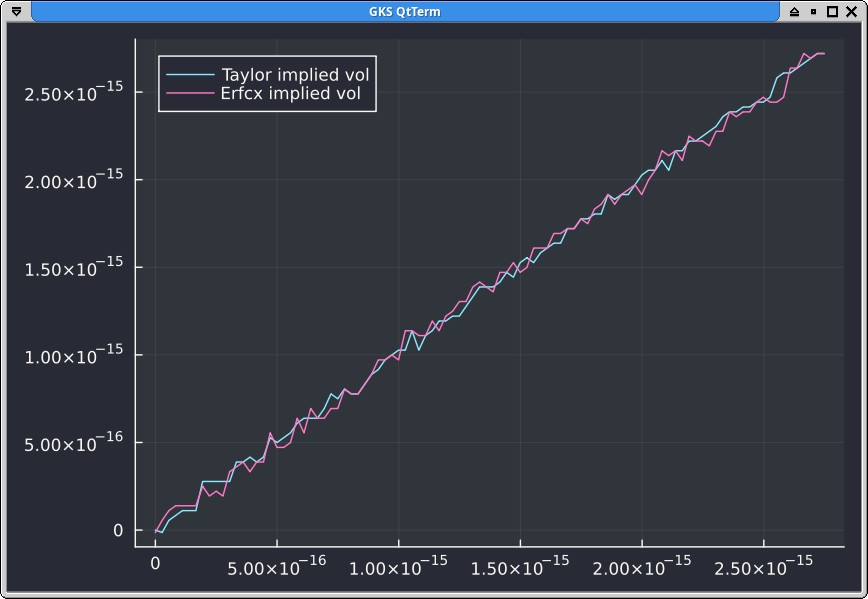
There is no visible difference in accuracy if we start from the erfcx prices and apply the SR Householder solver of Jherek Healy:

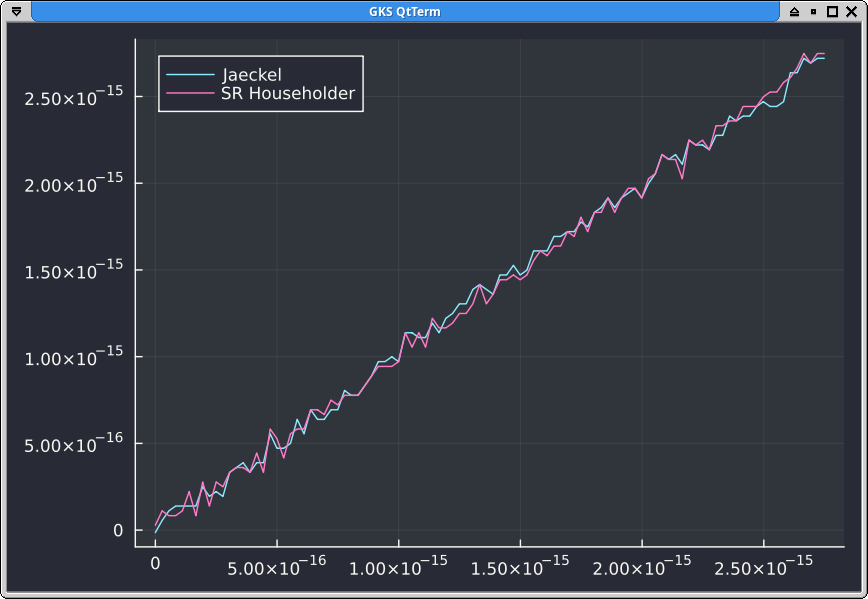
It should not be too surprising: if we compose the Black-Scholes formula with the associated solver from Peter Jaeckel, we do not obtain the identity function. Because the option prices are not monotonic with the vol, there are several vols which may be solution to the same price, and the solver is guaranteed to not solve exactly, which leads to the numerical noise we see on the plots. In contrast, it is remarkable that if we compose exp with log we have a nice monotonic shape:

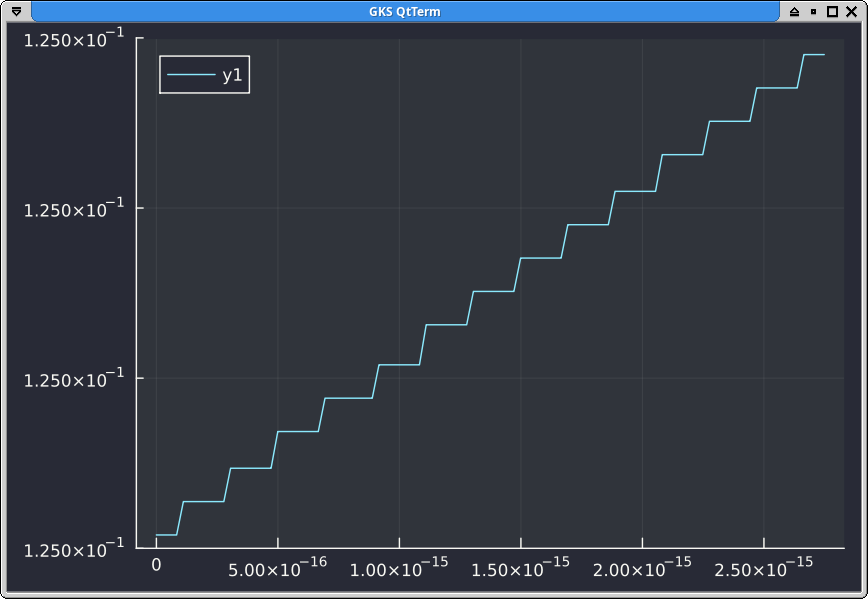
The prerequisite for a more accurate solver would be a Black-Scholes function which is actually monotonic.