Expansions for the time-dependent Heston model: Useless?
Fabrice Rouah wrote two books on the Heston model: one with C# and Matlab code, and one with VBA code. The two books are very similar. They are good in that they tackle most of the important points with the Heston model, from calibration to simulation. The calibration part (chapter 6) is a bit too short, it would have been great if it presented the actual difficulties with calibration in practice and went more in-depth with the techniques.
There is a full chapter on the time-dependent Heston model and it presents there the expansion of Benhamou, Gobet and Miri. The code is relatively annoying to write, so it’s great to have code available for it in the book. It is not so common for books to give source code with it, if you read the free access pages on Wiley’s website, you can download the source code.
Also the methodology used is the correct one to follow: first, reproduce the numbers of the original paper, second, use the approximation in a concrete calibration. There are however two major problems:
- The code has errors.
- The expansion is not really good in practice.
There are two errors in the code: one in the cross derivative of PHIgxy2 (first order on x and second order on y), and one in the second order cross derivative of the Black-Scholes price dPdx2dy2.
PHIgxy2 = (1/2)*y^(-2)*(phigx*(f+g/2-f^2*g/2) + phig*(fx+gx/2-f*fx*g/2-f^2*gx/2));PHIgxy2 = -(3/2)*y^(-2.5)*phig*(1-f*g)/2 + y^(-1.5)*phigy*(1-f*g)/2 - y^(-1.5)*phig*fy*g/2 - y^(-1.5)*phig*f*gy/2;and
dPdx2dy2 = K*exp(-rf*T(NT))*PHIfx2y2 - exp(-q*T(NT))*S*(PHIgy + 2*PHIgxy + PHIgx2y + PHIgy2 + 2*PHIgxy2 + PHIgx2y2);should be
dPdx2dy2 = K*exp(-rf*T(NT))*PHIfx2y2*PHIfx2y2 - exp(-q*T(NT))*S*(PHIgy2 + 2*PHIgxy2 + PHIgx2y2);The formula for the piecewise-constant coefficients also contains errors: for example, the total variance variable wT is wrong. It should be a double sum instead of the standard constant Heston like formula. Finally, the many sums are rederived in the book, differently from the paper and are not simplified (unlike in the paper where they are all single sums).
Indeed, with the original code from Rouah, the prices in the table of the paper from Benhamou Gobet and Miri are not reproduced to the last digit. With the above changes, they are.
On the second point, it is surprising that the book does not mention that the approximation is not great. In particular, it does not mention that the calibrated parameters between Table 9.6 and Table 9.3 are vastly different (except for v0). The calibrated smile is plotted, which is great, but it is only plotted with the approximation formula. Plotting the same using the nearly exact semi-analytical representation of vanlla option prices would have been enlightening. We do it below, as Fabrice Rouah gives all the inputs (a very good thing):
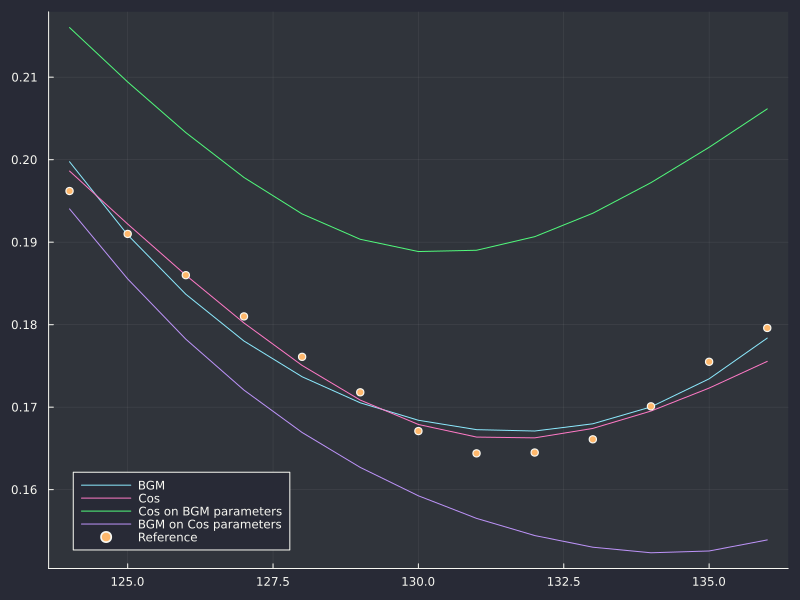
DJIA 37 days maturity.
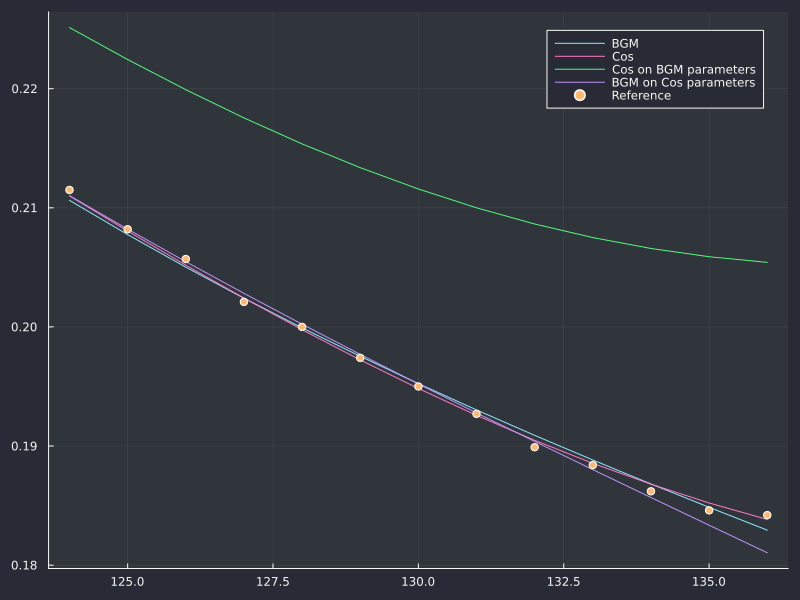
DJIA 226 days maturity.
It looks like in the range the calibration stays in the range of applicability of the formula, which is good, but not necessarily always true. The main issue is however that the calibrated parameters with the approximation are not necessarily a good guess for the parameters of the true time-dependent Heston model, precisely because the actual optimal parameters are way outside the range where the approximation is accurate. This is clear in the 226D plot, the best fit from the approx (which is great) ends up a not so good fit for the real time-dependent Heston model. Somewhat interestingly, the approx is actually not so bad on the actual optimal parameters, gotten from a calibration of the model with the Cos method - it is however a less good fit with the approx than the optimal parameters gotten from a calibration of the model with the approximation.
More recently, Pat Hagan proposed a new approximation for the model, based on a SABR mapping. It seems a bit more precise than the approximation of Benhamou Gobet and Miri, but is not great either. And it is disappointing that the paper does not present any number, nor any plot to assess the quality of the approximation given. Van der Zwaard gives some relatively realistic yet simple set of parameters for the Heston model (using Hagan’s reparameterization with constant expected variance = 1) and on those, the approximated prices of at-the-money options are just not usable:
If we consider his Table 5.9 (maturity = 1.75 year), we have the following
| Method | Price | Error |
|---|---|---|
| BGM | 4.2206 | 0.21 |
| Hagan | 3.3441 | 0.66 |
| Reference | 4.0039 | 0 |
With Table 5.10 (maturity = 1.3 year), it is even worse:
| Method | Price | Error |
|---|---|---|
| BGM | 0.6659 | 1.17 |
| Hagan | 0.2263 | 1.61 |
| Reference | 1.8407 | 0 |