Variance Swap Term-Structure under Schobel-Zhu
I never paid too much attention to it, but the term-structure of variance swaps is not always realistic under the Schobel-Zhu stochastic volatility model.
This is not fundamentally the case with the Heston model, the Heston model is merely extremely limited to produce either a flat shape or a downward sloping exponential shape.
Under the Schobel-Zhu model, the price of a newly issued variance swap reads $$ V(T) = \left[\left(v_0-\theta\right)^2-\frac{\eta^2}{2\kappa}\right]\frac{1-e^{-2\kappa T}}{2\kappa T}+2\theta(v_0-\theta)\frac{1-e^{-\kappa T}}{\kappa T}+\theta^2+\frac{\eta^2}{2\kappa},,$$ where \( \eta \) is the vol of vol.
When \( T \to \infty \), we have \( V(T) \to \theta^2 + \frac{\eta^2}{2\kappa} \). Unless \( \kappa \) is very large, or the vol of vol is very small, the second term will often dominate. In plain words, the prices of long-term variance swaps are almost purely dictated by the vol of vol when the speed of mean reversion is lower than 1.0.
Below is an example of fit to the market. If the vol of vol and kappa are exogeneous and we calibrate only the initial vol v0, plus the long term vol theta to the term-structure of variance swaps, then we end up with upward shapes for the term-structure, regardless of theta. Only when we add the vol of vol to the calibration, we find a reasonable solution. The solution is however not really better than the one corresponding to the Heston fit with only 2 parameters. It thus looks overparameterized.
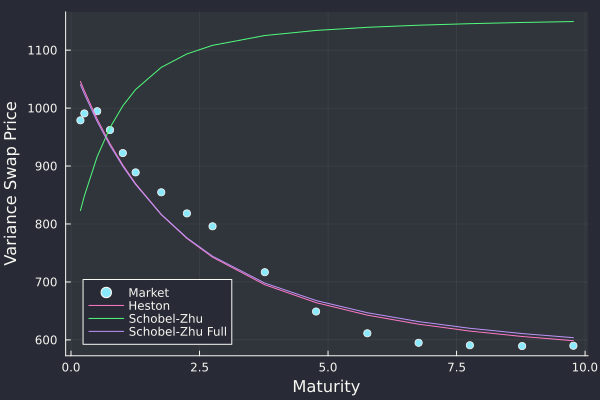
Term-structure of variance swap prices on Russell 2000 index
There are some cases where the Schobel-Zhu model allows for a better fit than Heston, and makes use of the flexibility due to the vol of vol.
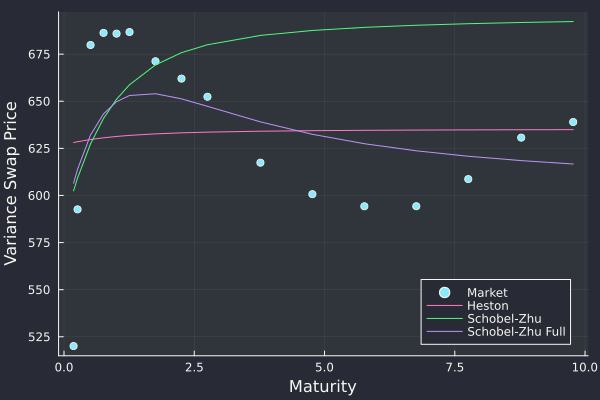
Term-structure of variance swap prices on SPX 500 index
It is awkward that the variance swap term-structure depends on the vol of vol in the Schobel-Zhu model.