Unintuitive behavior of the Black-Scholes formula - negative volatilities in displaced diffusion extrapolation
I am looking at various extrapolation schemes of the implied volatilities. An interesting one I stumbled upon is due to Kahale. Even if his paper is on interpolation, there is actually a small paragraph on using the same kind of function for extrapolation. His idea is to simply lookup the standard deviation \( \Sigma \) and the forward \(f\) corresponding to a given market volatility and slope: $$ c_{f,\Sigma} = f N(d_1) - k N(d_2)$$ with $$ d_1 = \frac{\log(f/k)+\Sigma^2 /2}{\Sigma} $$
We have simply: $$ c’(k) = - N(d_2)$$
He also proves that we can always find those two parameters for any \( k_0 > c_0 > 0, -1 < c_0’ < 0 \)
Then I had the silly idea of trying to match with a put instead of a call for the left wing (as those are out-of-the-money, and therefore easier to invert numerically). It turns out that it works in most cases in practice and produces relatively nice looking extrapolations, but it does not always work. This is because contrary to the call, the put value is bounded with \(f\). $$ p_{f,\Sigma} = k N(-d_2) - f N(-d_1)$$
Inverting \( p_0’ \) is going to lead to a specific \( d_2 \), and you are not guaranteed that you can push \( f \) high and have \( p_{f, \Sigma} \) large enough to match \( p_0 \). As example we can just take \(p_0 \geq k N(-d_2)\) which will only be matched if \( f \leq 0 \).
This is slightly unintuitive as put-call parity would suggest some kind of equivalence. The problem here is that we would need to consider the function of \(k\) instead of \(f\) for it to work, so we can’t really work with a put directly.
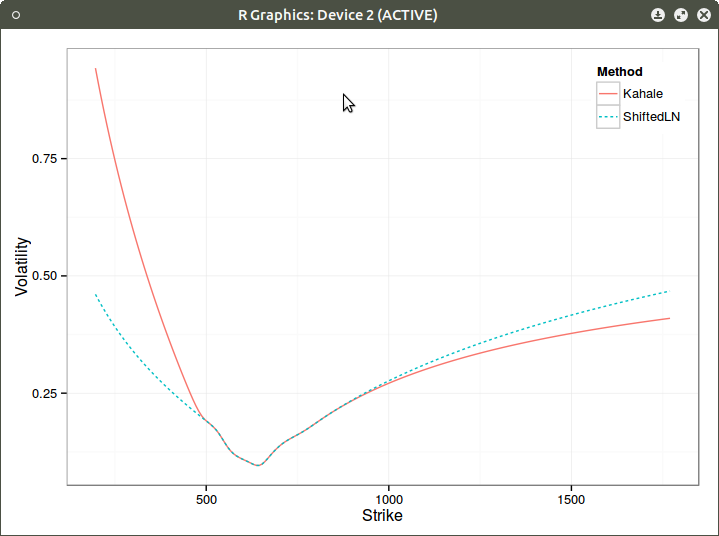
Here are the two different extrapolations on Kahale own example:

Window Extrapolation of the left wing with calls (blue doted line)
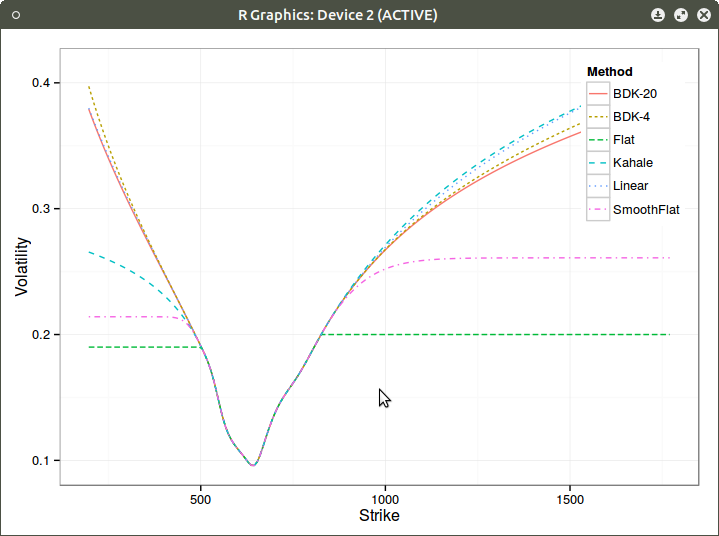
Extrapolation of the left wing with puts (blue doted line)
Displaced diffusion extrapolation is sometimes advocated. It is not the same as Kahale extrapolation: In Kahale, only the forward variable is varying in the Black-Scholes formula, and there is no real underlying stochastic process. In a displaced diffusion setting, we would adjust both strike and forward, keeping put-call parity at the formula level. But unfortunately, it suffers from the same kind of problem: it can not always be solved for slope and price. When it can however, it will give a more consistent extrapolation. I find it interesting that some smiles can not be extrapolated by displaced diffusion in a C1 manner except if one allows negative volatilities in the formula (in which case we are not anymore in a pure displaced diffusion setting).