The COS method for Heston
Fang, in her thesis, has the idea of the COS method and applies it to Heston. There are several published papers around it to price options under various models that have a known characteristic function, as well as to price more exotic options like barriers or bermudans.
The COS method is very close to the more standard Heston quasi analytic formula (use transform of characteristic function for the density and integrates the payoff with the density, exchanging summation), except that the more simple Fourier series are used instead of the standard Fourier transform. As a consequence there are a few more approximations that are done related to the truncation of the domain of integration and the result is already discrete, so no need for a Gaussian quadrature.
In practice, the promise is to be faster. I was wondering how stable it was, especially with regards to short maturities/large strikes.
It’s quite easy to code, I made only one mistake initially: I forgot to handle the first element of the sum differently. It is however very unstable for call options prices, because the upper integration boundary is then used in an exponential, which explodes in most cases I have tried, while for put options, the lower boundary is used in an exponential, and the lower boundary is negative.
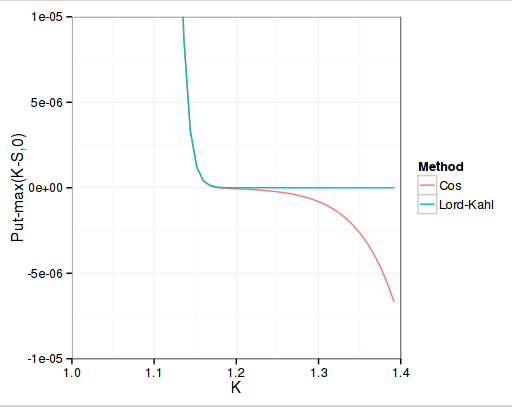
Price is too low at high strikes
So one has to rely on the put-call parity formula to compute call prices. This means that we are limited to something around machine epsilon accuracy and can’t compute a very out-of-the-money call price, contrary to the Lord-Kahl method. However it seemed stable for the various Heston parameters I have tried and accurate as long as the resulting price is not too small as the following graph shows.
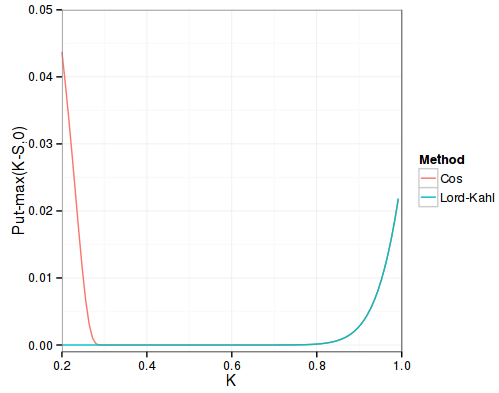
Price is way too high at low strikes
I was surprised to see that the more in-the-money put options also have inaccuracy: the price given is actually less than the final payoff. This is related to the domain of truncation. If I double it (L=24 instead of L=12), those disappear, what remains is that OTM puts can’t go beyond 1e-12 for the COS method.
In practice the COS method was effectively 2x to 3x faster than my Lord-Kahl implementation. As a side note, on this problem, Java is only 2x faster than Octave.
As long as we don’t care about very small option prices, it is an interesting alternative, especially because it is simple.
Update April 2014 - There is more information on the subject in my paper at http://papers.ssrn.com/abstract=2362968