SABR with Andreasen-Huge

Fri, May 24, 2013 I am on holiday today. Unfortunately I am still thinking about work-related matters, and out of curiosity, wanted to do a little experiment. I know it is not very good to spend free time on work related stuff: there is no reward for it, and there is so much more to life. Hopefully it will be over after this post.

Around 2 years ago, I saw a presentation from Andreasen and Huge about how they were able to price/calibrate SABR by a one-step finite difference technique. At that time, I did not understand much their idea. My mind was too focused on more classical finite differences techniques and not enough on the big picture in their idea. Their idea is quite general and can be applied to much more than SABR.

Recently there has been some talk and development going on where I work about SABR (a popular way to interpolate the option implied volatility surface for interest rate derivatives), especially regarding the implied volatility wings at low strike, and sometimes on how to price in a negative rates environment. There are actually quite a bit of research papers around this. I am not really working on that part so I just mostly listened. Then a former coworker suggested that the Andreasen Huge method was actually what banks seemed to choose in practice. A few weeks later, the Thalesians (a group for people interested in quantitative finance) announced a presentation by Hagan (one of the inventor of SABR) about a technique that sounded very much like Andreasen-Huge  to deal with the initial SABR issues in low rates.

As the people working on this did not investigate Andreasen-Huge technique, I somehow felt that I had to and that maybe, this time, I would be able to grasp their idea.

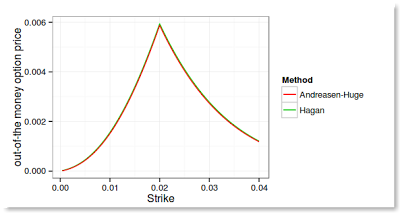
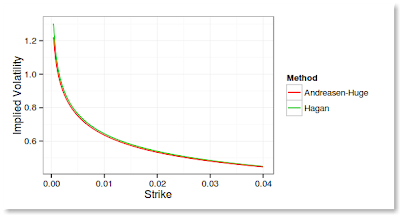
It took me just a few hours to have meaningful results. Here is the price of out of the money vanilla options using alpha = 0.0758194, nu = 0.1, beta = 0.5, rho = -0.1, forward = 0.02, and a maturity of 2 years.


I did not have in my home library a way to find the implied volatility for a given price. I knew of 2 existing methods, Jaeckel "By Implication", and Li rational functions approach. I discovered that Li wrote a new paper on the subject where he uses a SOR method to find the implied volatility and claims it's very accurate, very fast and very robust. Furthermore, the same idea can be applied to normal implied volatility. What attracted me to it is the simplicity of the underlying algorithm. Jaeckel's way is a nice way to do Newton-Raphson, but there seems to be so many things to "prepare" to make it work in most cases, that I felt it would be too much work for my experiment. It took me a few more hours to code Li SOR solvers, but it worked amazingly well for my experiment.



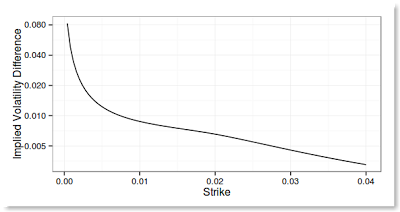
At first I had an error in my boundary condition and had no so good results especially with a long maturity. The traps with Andreasen-Huge technique are very much the same as with classical finite differences: be careful to place the strike on the grid (eventually smooth it), and have good boundaries.