Roughness of Stochastic Volatility with Jumps
I was wondering if adding jumps to stochastic volatility, as is done in the SVCJ model of Duffie, Singleton and Pan “Transform Analysis and Asset Pricing for Affine Jump-Diffusion” also in Broadie and Kaya “Exact simulation of stochastic volatility and other affine jump diffusion processes”, would lead to rougher paths, or if it would mislead the roughness estimators.
The answer to the first question can almost be answered visually:
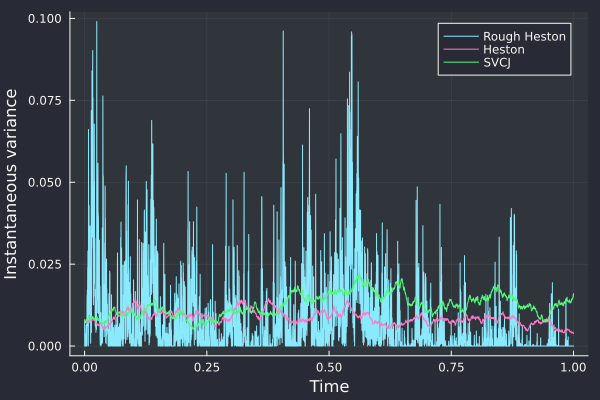
The parameters used are the one from Broadie and Kaya: v0=0.007569, kappa=3.46, theta=0.008, rho=-0.82, sigma=0.14 (Heston), jump correlation -0.38, jump intensity 0.47, jump vol 0.0001, jump mean 0.05, jump drift -0.1.
The Rough Heston with H=0.1 is much “noisier”. There is not apparent difference between SVCJ and Heston in the path of the variance.
The estimator of Cont and Das (on a subsampled path) leads to a Hurst exponent H=0.503, in line with a standard Brownian motion.
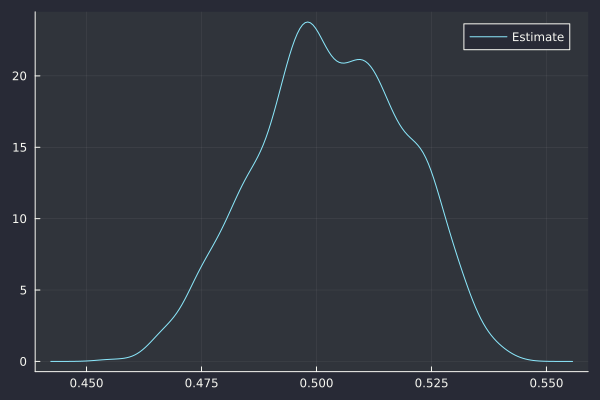
Cont-Das estimate H=0.503.
The estimator from Rosenbaum and Gatheral leads to a Hurst exponent (slope of the regression) H=0.520 with well behaved regressions:
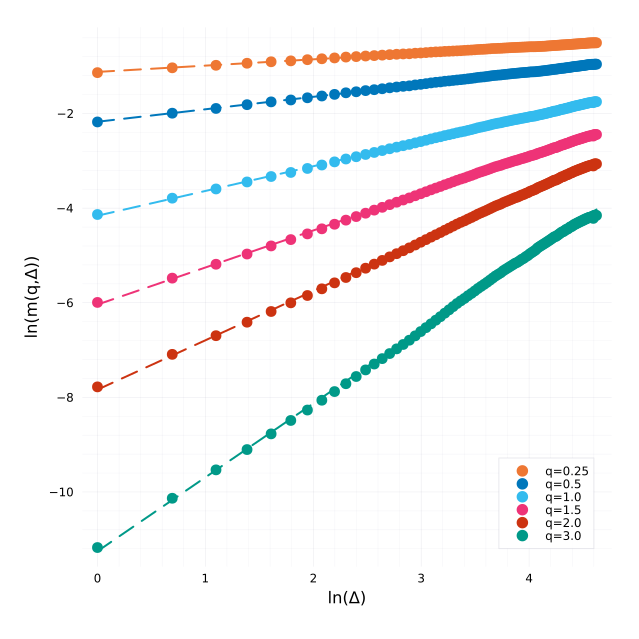
Regressions for each q.
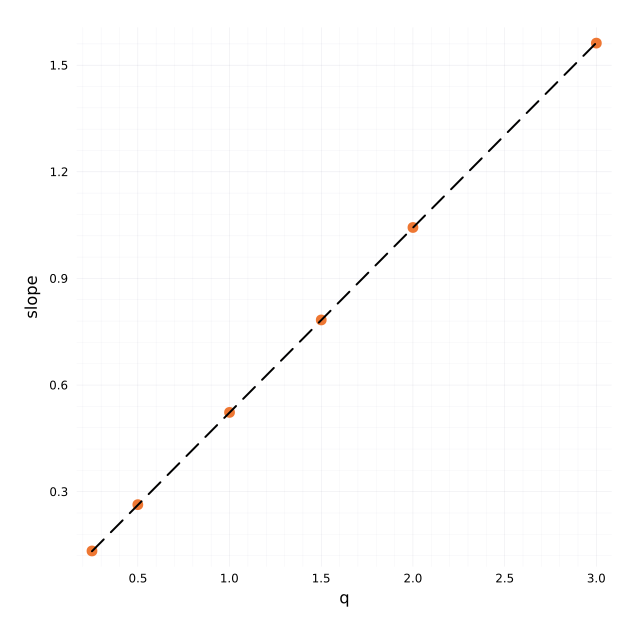
Regression over all qs which leads to the estimate of H.
On this example, there are relatively few jumps during the 1 year duration. If we multiply the jump intensity by 1000 and reduce the jump mean accordingly, the conclusions are the same. Jumps and roughness are fundamentally different.
Of course this does not mean that the short term realized volatility does not look rough as evidenced in Cont and Das paper:
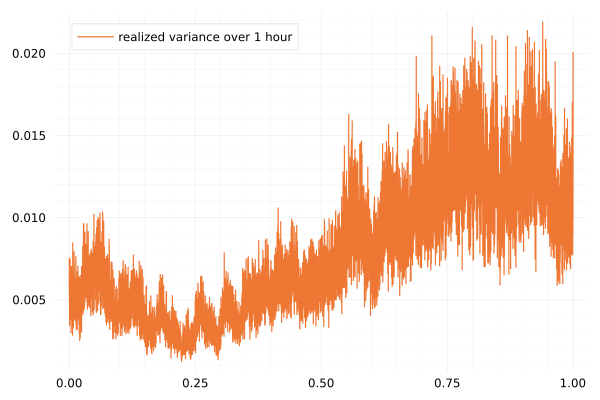
The 1 hour realized volatility looks rough.
It is not really rough, estimators will have a tough time leading to stable estimates on it.
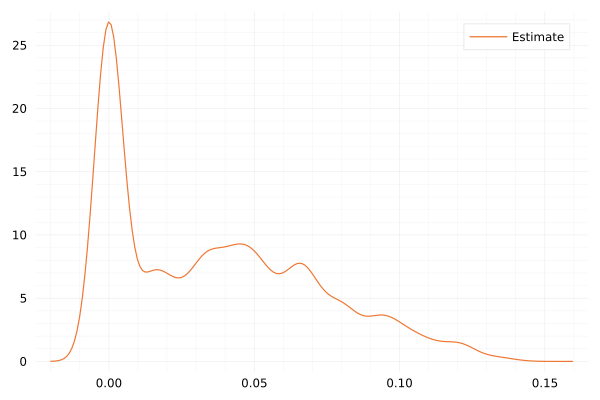
Hurst exponent estimation based on the 1h realized variance. The mean H=0.054 but is clearly not reliable.
This is very visible with the Rosenbaum-Gatheral way of estimating H, we see that the observations do not fall on a line at all but flatten:
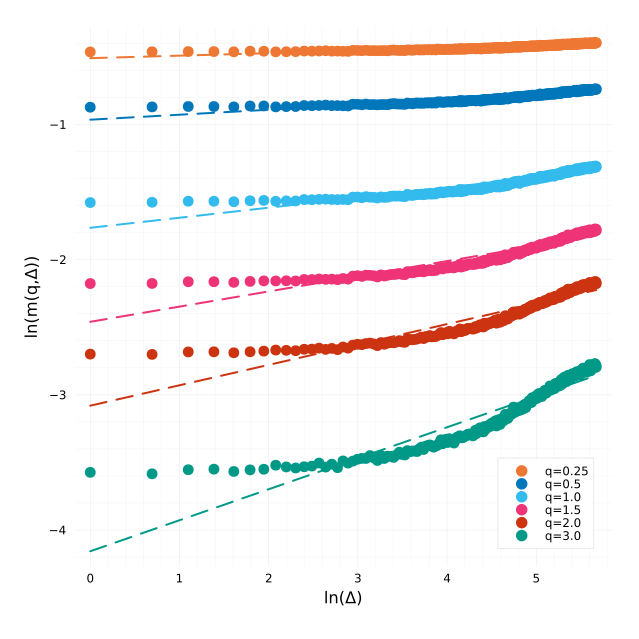
Regressions for each q based on the 1h realized variance.
The pure Heston model leads to similar observations.