Roughness of Pure Jumps
In my previous blog post, I looked at the roughness of the SVCJ stochastic volatility model with jumps (in the volatility). In this model, the jumps occur randomly, but at discrete times. And with typical parameters used in the litterature, the jumps are not so frequent. It is thus more interesting to look at the roughness of pure jump processes, such as the CGMY process.
The CGMY process is more challenging to simulate. I used the approach based on the characteristic function described in Simulating Levy Processes from Their Characteristic Functions and Financial Applications. Ballota and Kyriakou add some variations based on FFT pricing of the characteristic function in Monte Carlo simulation of the CGMY process and option pricing and pay much care about a proper truncation range. Indeed, I found that the truncation range was key to simulate the process properly and not always trivial to set up especially for \(Y \in (0,1) \). I however did not implement any automated range guess as I am merely interested in very specific use cases, and I used the COS method instead of FFT.
I also directly analyze the roughness of a sub-sampled asset path (the exponential of the CGMY process), and not of some volatility path as I was curious if pure jump processes would mislead roughness estimators. I simulated the paths corresponding to parameters given in Fang thesis The COS Method - An Efficient Fourier Method for Pricing Financial Derivatives: C = 1, G = 5, M = 5, Y = 0.5 or Y = 1.5.
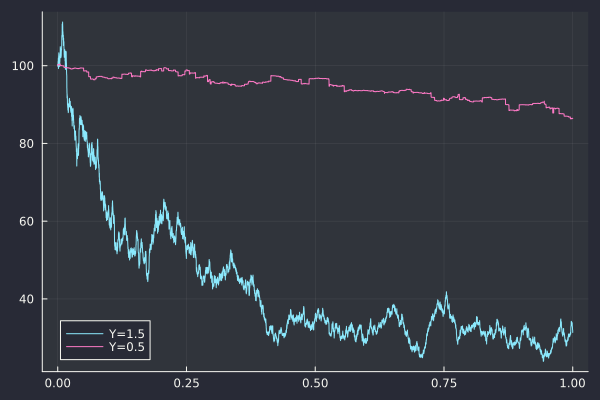
And the corresponding Hurst index estimate via the Cont-Das method:
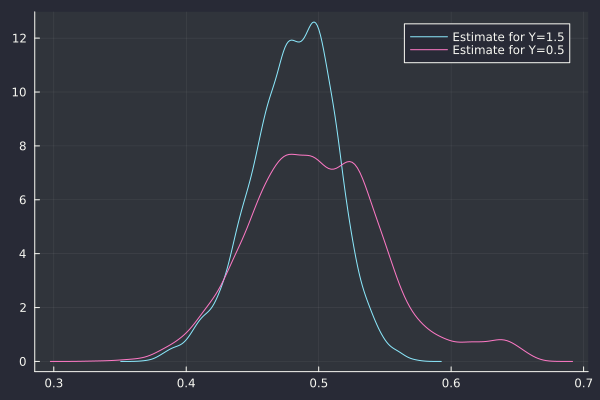
Similarly the Gatheral-Rosenbaum estimate has no issue finding H=0.5.