Fixing NaNs in Quadprog
Out of curiosity, I tried quadprog as open-source quadratic programming convex optimizer, as it is looks fast, and the code stays relatively simple. I however stumbled on cases where the algorithm would return NaNs even though my inputs seemed straighforward. Other libraries such as CVXOPT did not have any issues with those inputs.
Searching on the web, I found that I was not the only one to stumble on this kind of issue with quadprog. In particular, in 2014, Benjamen Tyner gave a simple example in R, where solve.QP returns NaNs while the input is very simple: an identity matrix with small perturbations out of the diagonal. Here is a copy of his example:
library(quadprog)
n <- 66L
set.seed(6860)
X <- matrix(1e-20, n, n)
diag(X) <- 1
Dmat <- crossprod(X)
y <- seq_len(n)
dvec <- crossprod(X, y)
Amat <- diag(n)
bvec <- y + runif(n)
sol <- solve.QP(Dmat, dvec, Amat, bvec, meq = n)
print(sol$solution) # this gives all NaNsOther people stumbled on similar issues.
In my specific case, I was able to debug the quadprog algorithm and find the root cause: two variables \(g_c\) and \(g_s\) can become very small, and their square becomes essentially zero, creating a division by zero. If, instead of computing \( \frac{g_s^2}{g_c^2} \) we compute \( \left(\frac{g_s}{g_c}\right)^2 \), then the division by zero is avoided as the two variables are of the same order.
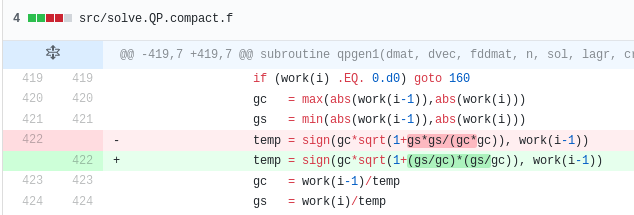
Sample code change [on github](https://github.com/cran/quadprog/pull/1/commits/7f51915f7c662c7fac3d4e2ab067cfbc292767f8).
While it probably does not catter for all the possible NaN use cases, it did fix all the cases I stumbled upon.