NUFFT and COS
Leif Andersen and Mark Lake recently proposed the use of Non-Uniform Fast Fourier Transform for option pricing via the characteristic function. Fourier techniques are most commonly used for pricing vanilla options under the Heston model, in order to calibrate the model. They can be applied to other models, typically with known characteristic function, but also with numerically solved characteristic function as in the rough Heston model, and to different kind of payoffs, for example variance/volatility swaps, options. The subject has been vastly explored already so what’s new with this paper?
At first, it was not obvious to me. The paper presents 3 different approaches, two where the probability density and cumulative density is first computed at a (not so sparse) set of knots and the payoff is integrated over it. The remaining approach is the classic one presented in the Carr and Madan paper from 1999 as well as in most of the litterature on the subject. The only additional trick is really the use of NUFFT along with some clever adaptive quadrature to compute the integral.
I thought the main cost in the standard Fourier techniques was the evaluation of the characteristic function at many points, because the characteristic function is usually relatively complicated. And, in practice, it mainly is. So what does the new NUFFT algorithm bring? Surely the characteristic function must still be evaluated at the same points.
The NUFFT becomes interesting to compute the option price at many many strikes at the same time. The strikes do not need to be equidistant and can be (almost) arbitrarily chosen. In Andersen and Lake paper, even a very fast technique such as the COS method reaches a threshold of option per second throughput, as the number of strikes is increased, mainly because of the repeated evaluation of the sum over different strikes, so the cost becomes proportional to the number of strikes.
Evaluating at many many points becomes not much more expensive than evaluating at a few points only. This is what opens up the possibilities for the first 2 approaches based on the density.
It turns out that it is not very difficult to rewrite the COS method so that it can make use of the NUFFT as well. I explain how to do it here. Below is the throughput using NFFT.jl Julia package:
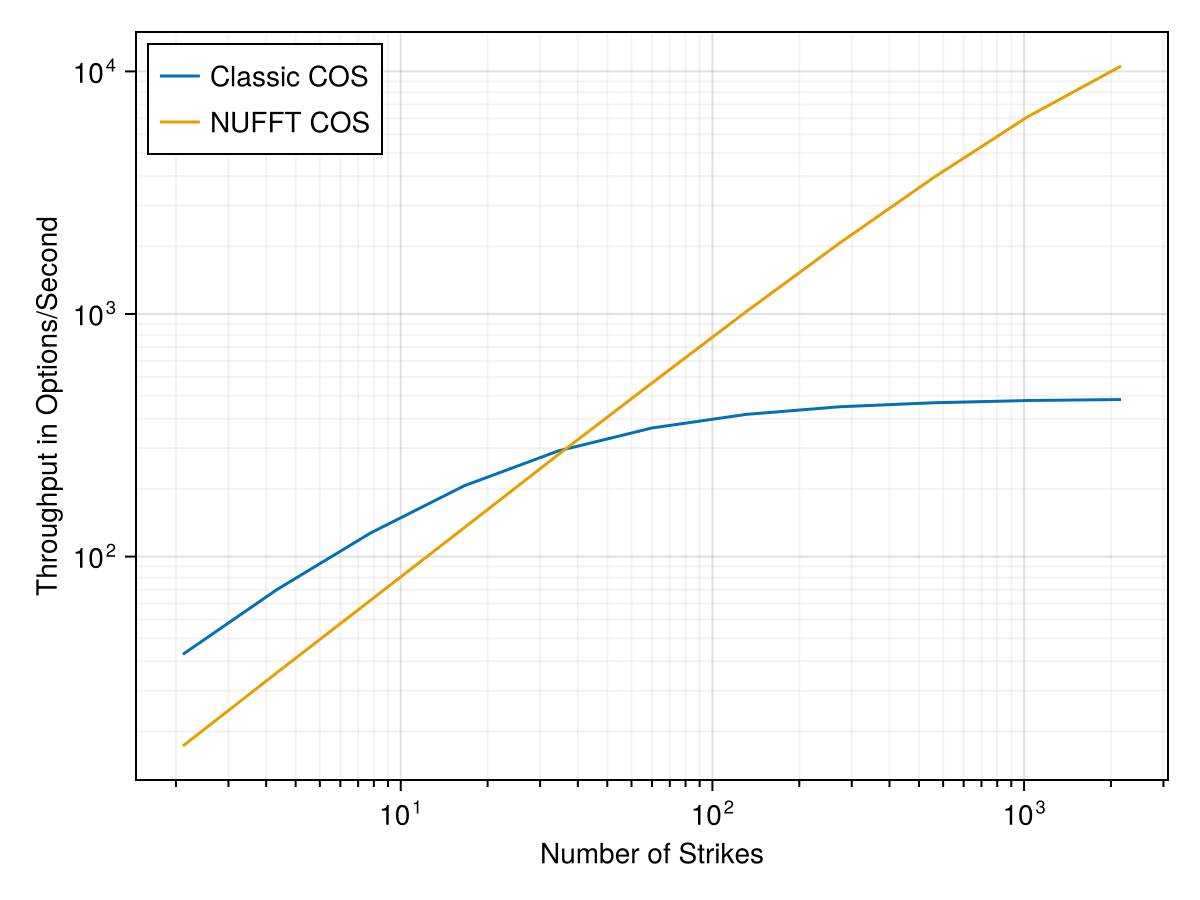
Throughput on the Heston model with M=256 points.
While a neat trick, it is however not 100% clear to me at this point where this is really useful: calibration typically involve a small number of strikes per maturity.