New Approximations for the Prices of Asian and basket Options
Many years ago, I had applied the stochastic expansion technique of Etore and Gobet to a refined proxy, in order to produce more accurate prices for vanilla options with cash dividends under the Black-Scholes model with deterministic jumps at the dividend dates. Any approximation for vanilla basket option prices can also be applied on this problem, and the sophisticated Curran geometric conditioning was found to be particularly competitive in The Pricing of Vanilla Options with Cash Dividends as a Classic Vanilla Basket Option Problem.
Recently, I had the idea of applying the same stochastic expansion technique to the prices of Asian options, and more generally to the prices of vanilla basket options. It works surprising well for Asian options. A main advantage is that the expansion is straightforward to implement: there is no numerical solving or numerical quadrature needed.
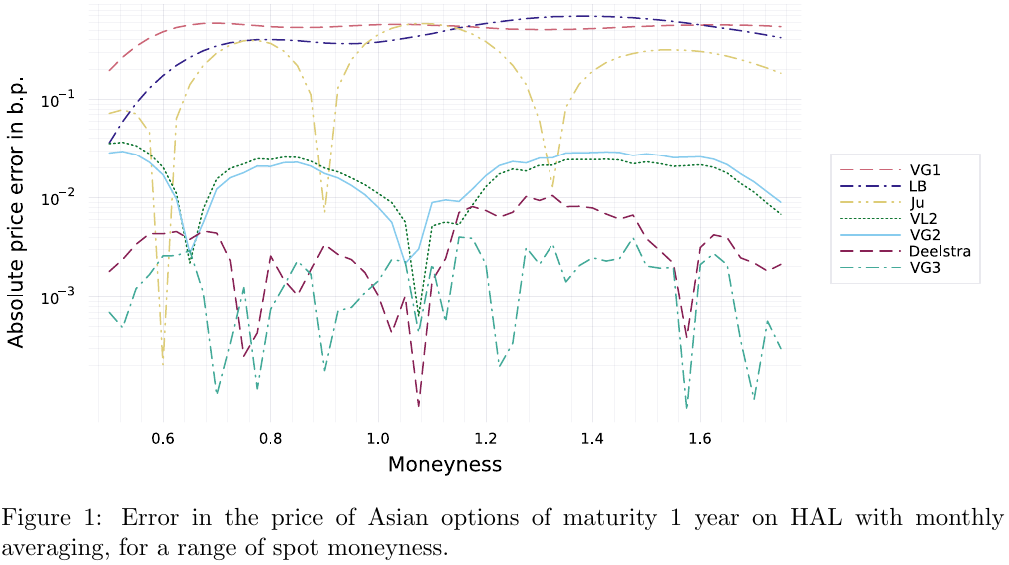
VGn and VLn are stochastic expansions of order n using two different proxies
It works a little bit less well for basket options. Even though I found a better proxy for those, the expansions behave less well with large volatility (really, large total variance), regardless of the proxy. I notice now this was also true for the case of discrete dividends where, clearly the accuracy deteriorates somewhat significantly in “extreme” examples such as a vol of 80% for an option maturity of 1 year (see Figure 3).
I did not compare the use of the direct stochastic expansion for discrete dividends, and the one going through the vanilla basket expansion, maybe for a next post.