More SVI Initial Guesses
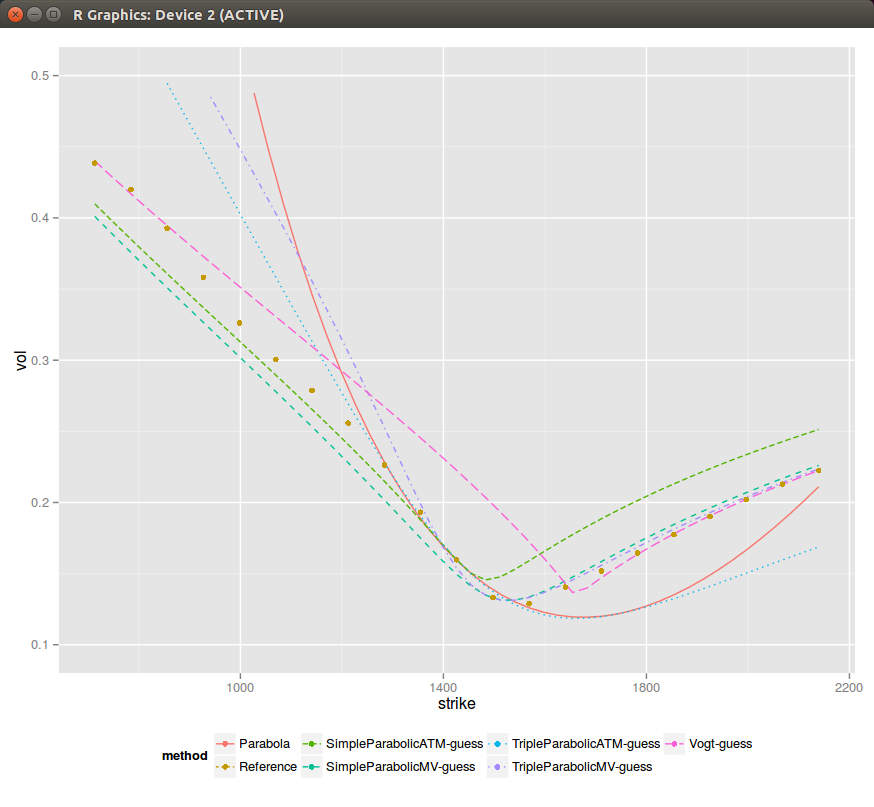
In the previous post, I showed one could extract the SVI parameters from a best fit parabola at-the-money. It seemed to work reasonably well, but I found some real market data where it can be much less satisfying.Sometimes (actually not so rarely) the ATM slope and curvatures can't be matched given rho and b found through the asymptotes. As a result if I force to just match the curvature and set m=0 (when the slope can't be matched), the simple ATM parabolic guess looks shifted. It can be much worse than this specific example.
It is then a bit clearer why Vogt looked to match the lowest variance instead of ATM. We can actually also fit a parabola at the lowest variance (MV suffix in the graph) instead of ATM. It seems to fit generally better.
I also tried to estimate the asymptotic slopes more precisely (using the slope of the 5-points parabola at each end), but it seems to not always be an improvement.
However this does not work when rho is close to -1 or 1 as there is then no minimum. Often, matching ATM also does not work when rho is -1 or 1. This specific case, but quite common as well for longer expiries in equities need more thoughts, usually a constant slice is ok, but this is clearly where Zeliade's quasi explicit method shines.
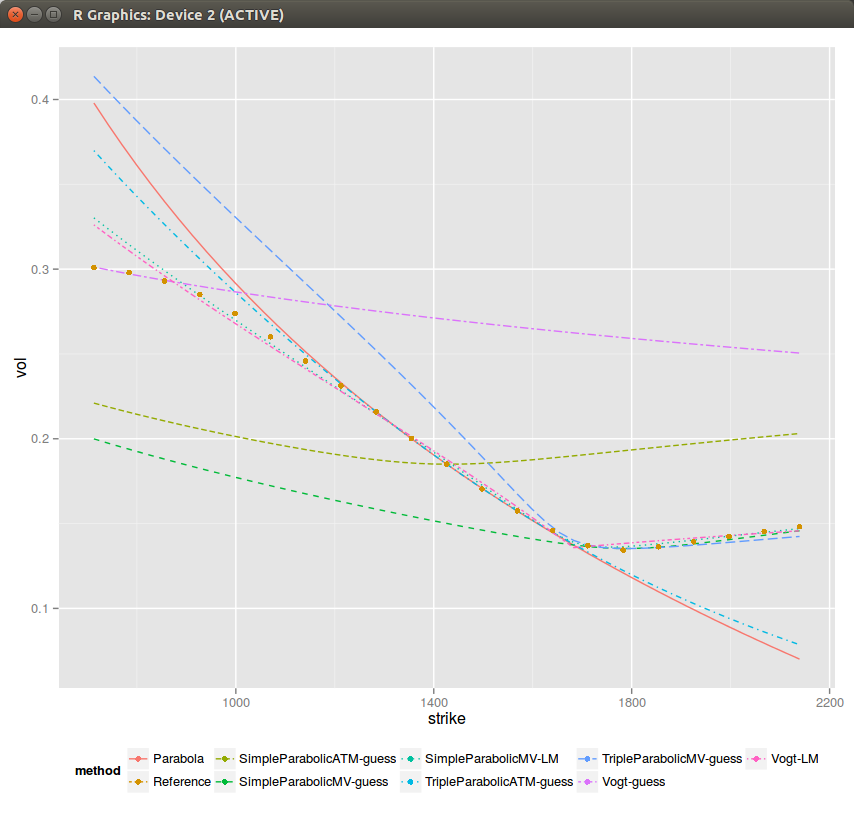
So far it still all looks good, but then looking at medium maturities (1 year), sometimes all initial guesses don't look comforting (although Levenberg-Marquardt minimization still works on those - but one can easily imagine that it can break as well, for example by tweaking slightly the rho/b and look at what happens then).
There is lots of data on this 1 year example. One can clearly see the problem when the slope can not be fitted ATM (SimpleParabolicATM-guess), and even if by chance when it can (TripleParabolicATM-guess), it's not so great.
Similarly fitting the lowest variance leads only to a good fit of the right wing and a bad fit everywhere else.
Still, as if by miracle, everything converges to the best fit on this example (again one can find cases where some guesses don't converge to the best fit). I have added some weights +-20% around the money, to ensure that we capture the ATM behavior accurately (otherwise the best fit is funny).
It is interesting to see that if one minimizes the min square sum of variances (what I do in Vogt-LM, it's in theory slightly faster as there is no sqrt function cost) it results in an ugly looking steeper curvature, while if we just minimize the min square sum of volatilities (what I do in SimpleParabolicMV_LM), it looks better.