Large Steps in Schobel-Zhu/Heston the Lazy Way

Fri, May 17, 2013 Van Haastrecht, Lord and Pelsser present an effective way to price derivatives by Monte-Carlo under the Schobel-Zhu model (as well as under the Schobel-Zhu-Hull-White model). It's quite similar to Andersen QE scheme for Heston in spirit.

In their paper they evolve the (log) asset process together with the volatility process, using the same discretization times. A while ago, when looking at  Joshi and Chan large steps for Heston, I noticed that, inspired by Broadie-Kaya exact Heston scheme, they present the idea to evolve the variance process using small steps and the asset process using large steps (depending on the payoff) using the integrated variance value computed by small steps. The asset steps correspond to payoff evaluation dates  At that time I had applied this idea to Andersen QE scheme and it worked reasonably well.

So I tried to apply the same logic to Schobel Zhu, and my first tests show that it works too. Interestingly, the speed gain is about 2x. Here are the results for a vanilla call option of different strikes.

Similar Error between long and short asset steps

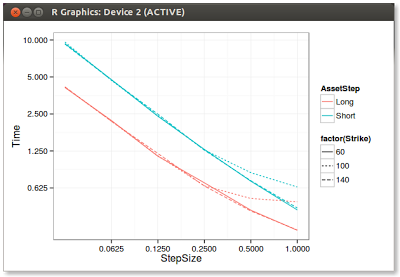Long steps take around 1/2 the time to compute

I would have expected the difference in performance to increase when the step size is decreasing, but it's not the case on my computer.

It's not truly large steps like Joshi and Chan do in their integrated double gamma scheme as the variance is still discretized in relatively small steps in my case, but it seems like a good, relatively simple optimization. A while ago, I did also implement the full Joshi and Chan scheme, but it's really interesting if one is always looking for long steps: it is horribly slow when the step size is small, which might occur for many exotic payoffs, while Andersen QE scheme perform almost as well as log-Euler in terms of computational cost.