Jumps impact: Variance swap vs volatility swap
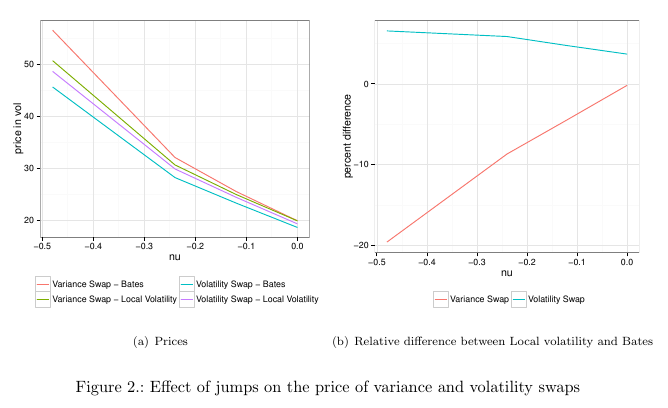
Beside the problem with the discreteness of the replication, variance swaps are sensitive to jumps. This is an often mentioned reason for the collapse of the single name variance swap market in 2008 as jumps are more likely on single name equities.
Those graphs are the result of Monte-Carlo simulations with various jump sizes using the Bates model, and using Local Volatility implied from the Bates vanilla prices. The local volatility price will be the same price as per static replication for the variance swap, and we can see it they converge when there is no jump.
The presence of jumps lead to a theoretically higher variance swap price, again, which we miss completely with the static replication. As jumps go higher, the difference is more pronounced.
Volatility swaps are a bit better behaved in this regard. Interestingly, local volatility overestimate the value in this case (which for variance swaps it underestimates the value). I also noticed that the relatively recent formula from Carr-Lee will underestimate jumps even more so than local volatility: it is more precise in the absence of jumps, very close to Heston, but less precise than local volatility when jumps increase in size.
I have added a small section around this in my paper on SSRN.