Calibrating Heston to Variance Swaps - a bad idea?
An interesting idea to calibrate the Heston model in a more stable manner and reduce the calibration time is to make use of variance swap prices. Indeed, there is a simple formula for the theoretical price of a variance swap in the Heston model.
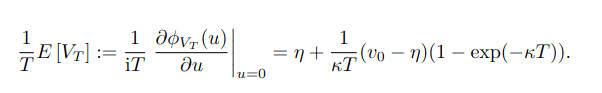
The idea was studied in the paper Heston model: the variance swap calibration by F. Guillaume and W. Schoutens back in 2014. The authors however only used the variance swap calibration as an initial guess. How bad would it be to fix the parameters altogether, as in a variance curve approach?
It turns out it can be quite bad since the Heston model does not allow to represent many shapes of the variance swap term structure. Below is an example of term-structure calibration on SPX as of October 2024.
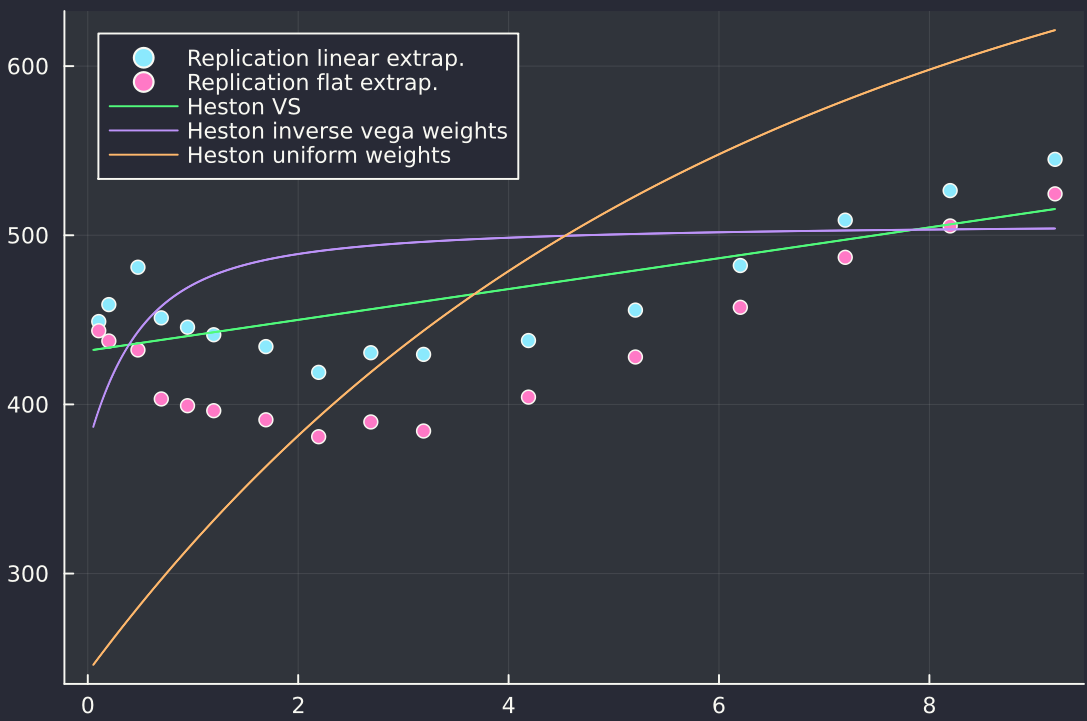
Term-structure of variance swap prices.
The term-structure is V-shaped, and Heston can not fit well to this. The best fit leads to non-sensical parameters with a nearly zero kappa (mean reversion speed) and an exploding long-term mean theta. The next figure shows why it is non-sensical: because the kappa is very small, the variance will very often reach zero.
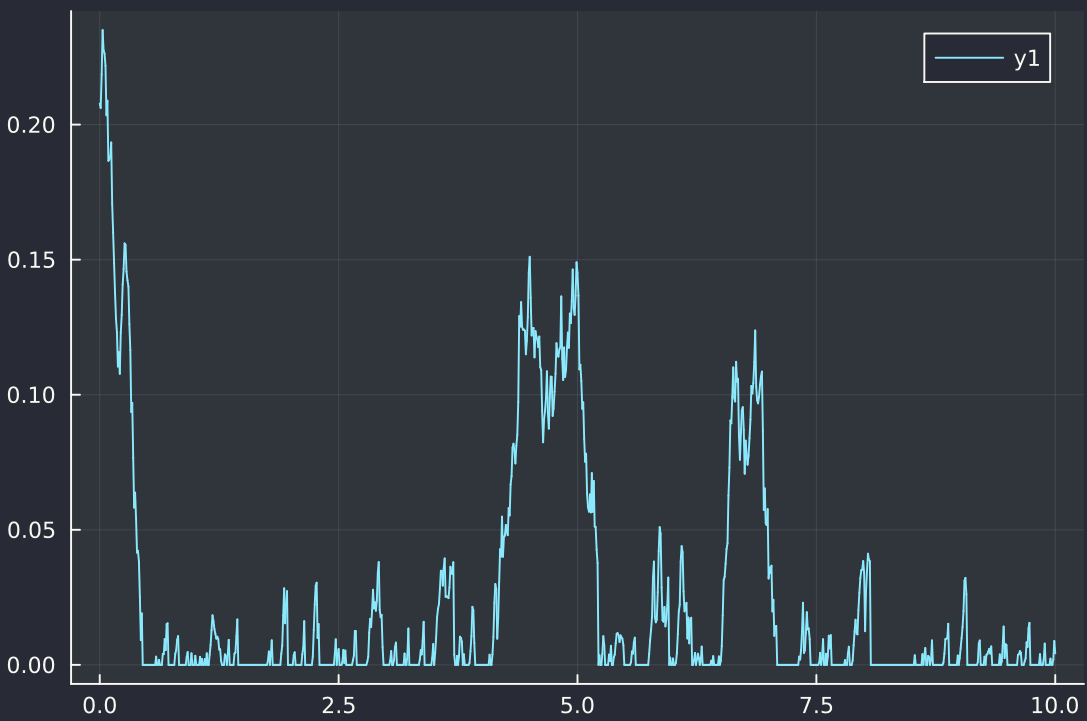
Sample path of the variance process (in terms of vol) using the Euler scheme with full truncation.
The calibration using inverse vega weights on vanilla option prices leads a not much worse fit of the variance swap term structure, but exhibits a much to high, unrealistic vol-of-vol of 184%, while a calibration on equally weighted option prices does not fit the term structure well at all.
Somewhat interestingly, the Double-Heston model allows to fit the term-structure much better, but it is far from obvious that the resulting calibrated parameters are much more realistic as it typically leads to process with very small kappa or a process with very small theta (but as there are two processes, it may be more acceptable).
Previously, I had explored a similar subject for the Schobel-Zhu model. It turns out that Heston is not much more practical either.