Heston or Schobel-Zhu issues with short expiries

Thu, Jul 3, 2014 It's relatively well known that Heston does not fit the market for short expiries. Given that there are just 5 parameters to fit a full surface, it's almost logical that one part of the surface of it is not going to fit well the market.
I was more surprised to see how bad Heston or Schobel-Zhu were to fit a single short expiry volatility slice. As an example I looked at SP500 options with 1 week expiry. It does not really matter if one forces kappa and rho to constant values (even to 0) the behavior is the same and the error in fit does not change much.

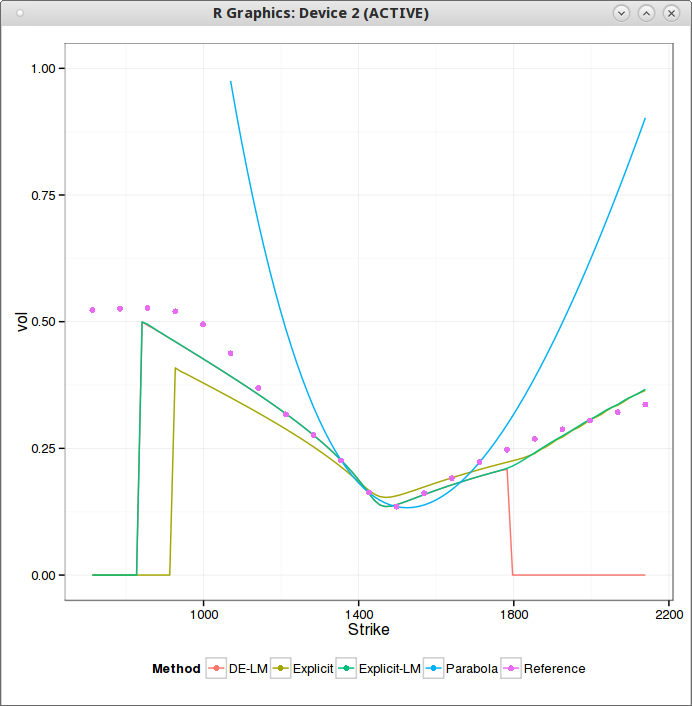Schobel-Zhu fit for a slice of maturity 1 week

In this graph, the brown, green and red smiles corresponds to Schobel-Zhu fit using an explicit guess (matching skew & curvature ATM), using Levenberg-Marquardt on this guess, and using plain differential evolution.
What happens is that the smiles flattens to quickly in the strike dimension. One consequence is that the implied volatility can not be computed for extreme strikes: the smile being too low, the price becomes extremely small, under machine epsilon and the numerical method (Cos) fails. There is also a bogus angle in the right wing, because of numerical error. I paid attention to ignore too small prices in the calibration by truncating the initial data.

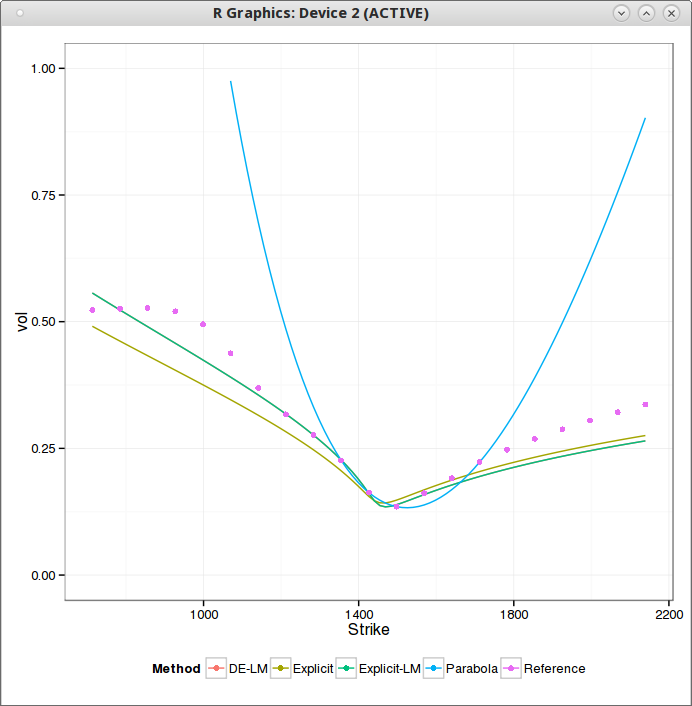Heston fit, with Lord-Kahl (exact wings)

SABR behaves much better (fixing beta=1 in this case) in comparison (As I use the same truncation as for Schobel-Zhu, the flat left wing part is ignored).

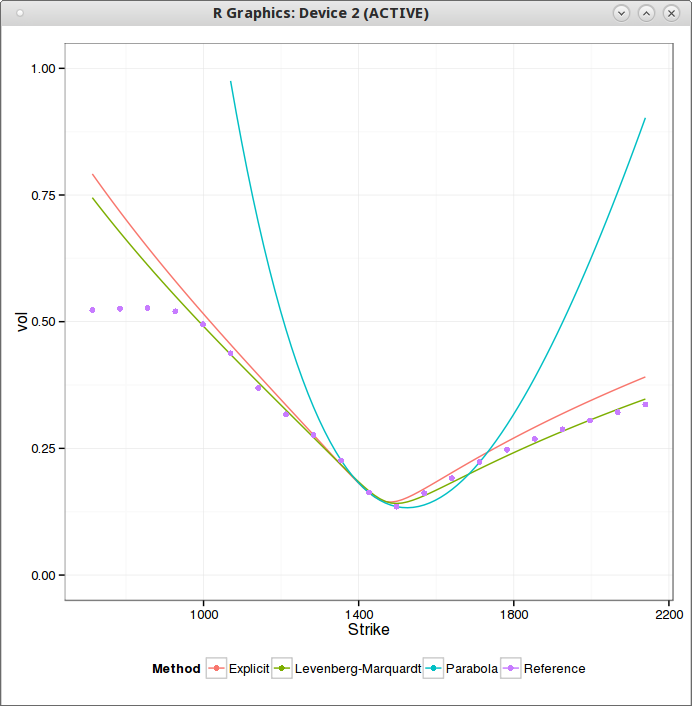SABR fit for a slice of maturity 1 week

For longer expiries, Heston & Schobel-Zhu, even limited to 3 parameters, actually give a better fit in general than SABR.