Ghost Vacations
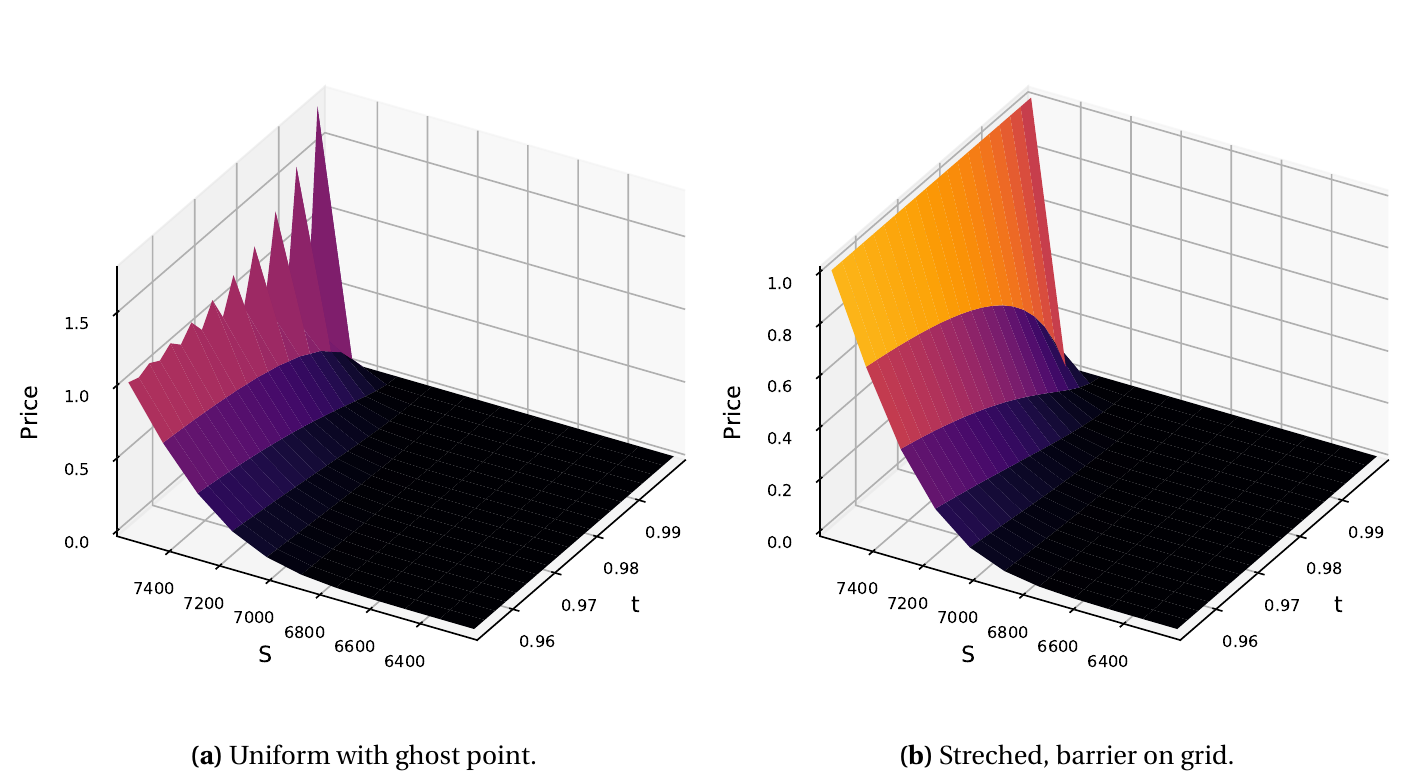
During my vacation, I don’t know why, but I looked at some stability issue with ghost points and the explicit method. I was initially trying out ghost points with the explicit runge kutta Chebyshev/Legendre/Gegenbauer technique and noticed some explosion in some cases.
I cornered it down to a stability issue of the standard explicit Euler method with ghost (or fictitious) points. The technique is described in the book “Paul Wilmott on Quantitative Finance” (also in Paul Wilmott introduces quantitative finance), which I find quite good, although I have some friends who are not much fond of it. The technique may be used to compute the price of a continuously monitored barrier option when the barrier does not fall on the grid, or more generally for time-dependent barriers. I however look at it in the simple context of a constant barrier in time.
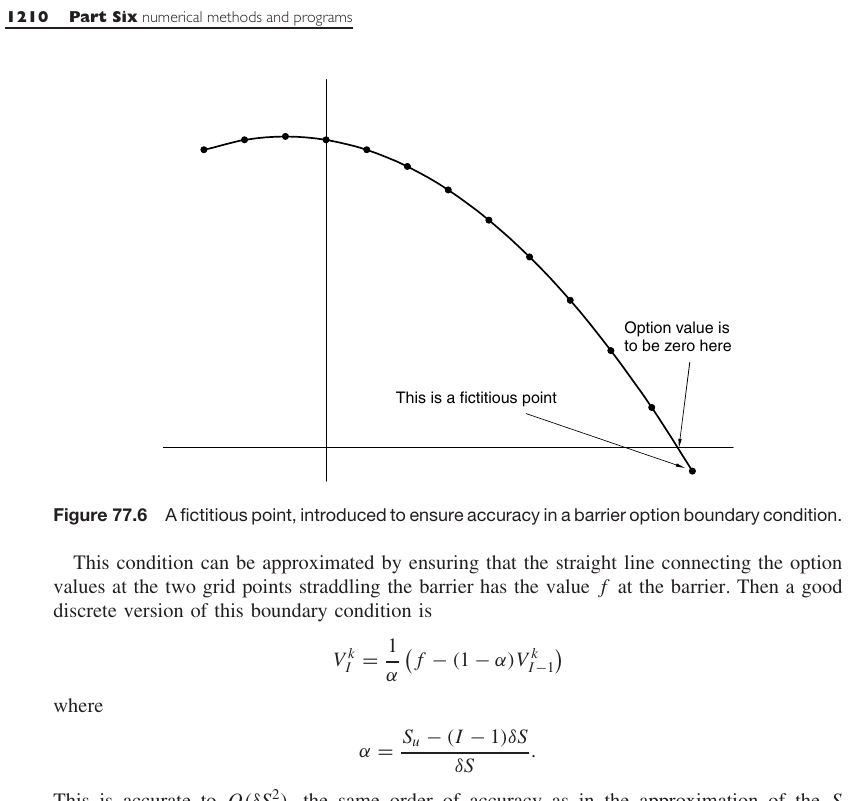
The ghost point technique (from Paul Wilmott on Quantitative Finance).
I found out that the explicit Euler scheme is unstable if we let the grid boundaries be random. In practice, for more exotic derivatives, the grid upper bound will typically be based on a number of standard deviations from the spot or from the strike price. The spot price moves continually, and the strike price is fairly flexible for OTC options. So the upper bound can really be anything and the explicit Euler may require way too many time-steps to be practical with the ghost point technique. This is all described in the preprint Instabilities of explicit finite difference schemes with ghost points on the diffusion equation.
What does this mean?
The ghost point technique is not appropriate for the explicit Euler scheme (and thus for the Runge-Kutta explicit schemes as well), unless the ghost point is fixed to be in the middle of the grid, or on the grid outside by one space-step. This means the grid needs to be setup in a particular fashion. But if we need to setup the grid such that the barrier falls exactly somewhere then, for a constant barrier option, no ghost point is needed, one just need to place the barrier on the grid and use a Dirichlet boundary condition.
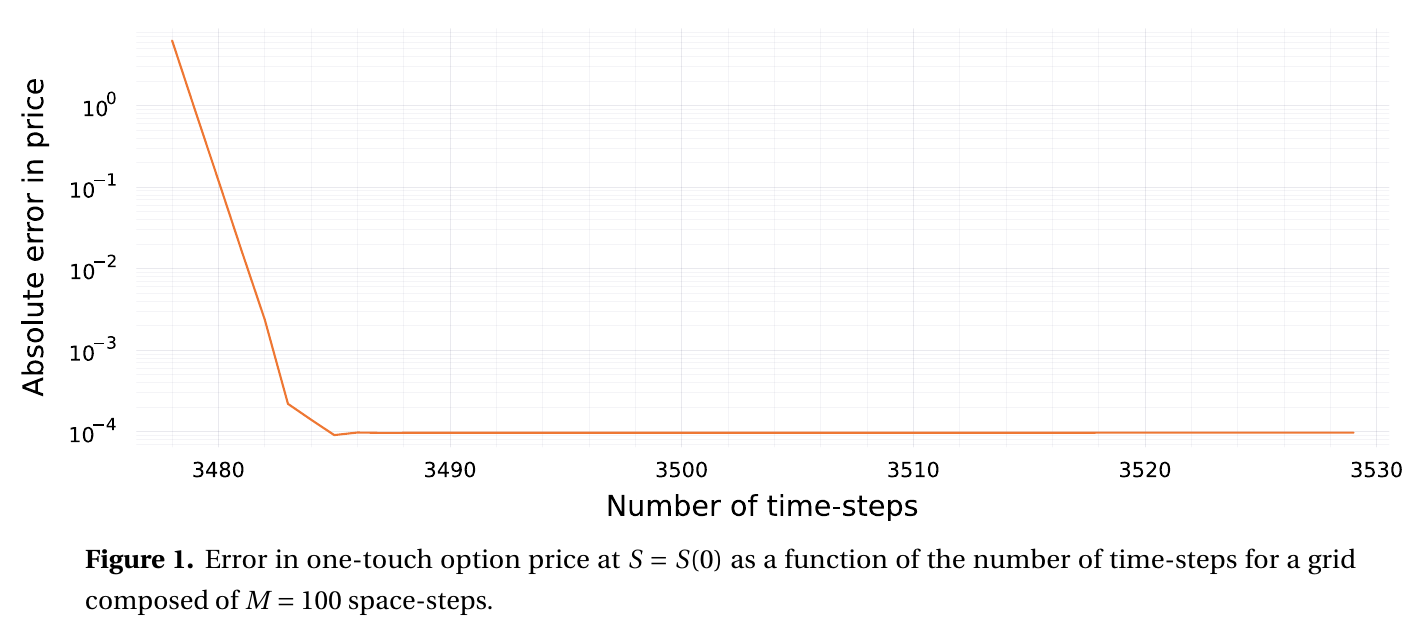
Explicit scheme requires a very large number of time-steps.