Forward Variance Models and Calibration
The modern rough volatility models adopt a forward variance curve terminology (see for example this paper on a rational approximation for the rough Heston, or this presentation on affine forward variance models or this paper on affine forward variance models). In this form, the rough Heston model reads:

According to the litterature, the initial forward variance curve is typically built from the implied volatilities through the variance swap replication: for each maturity, the price of a newly issued variance swap is computed to this maturity, using the implied volatilities for this maturity. Then we may compute the forward variance by interpolating linearly the variance swap prices and differentiating. This leads to the plot below.
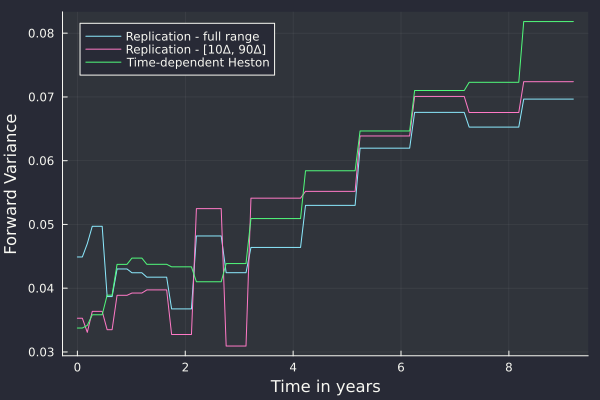
Forward variance curves for SPX500 as of October 2024.
One immediate question is how much does the truncation range play a role in this forward variance curve? Above, we plot the replications prices based on filtering the input data up to 10 Delta / 90 Delta for each maturity. Beyond this range, liquidity is usually much lower and the reliability of the input quotes may not be as good. The short end, and not so short forward variance up to 4 years is quite different. The long end is more aligned with something that looks like a basis spread between the two curves.
We may also calibrate the forward variance curve model directly to the implied volatilities during the model calibration, at the same time as the other stochastic volatility parameters (using a time-dependent correlation and vol-of-vol). This time-dependent Heston parameterization has effectively 3 parameters per expiry. In this case, we may want to also filter the input data to focus on the 10 Delta / 90 Delta range as we expect the stochastic volatility model to fit well where it matters the most - where the vanillas are liquid.
In the figure above, we also plot the forward variance curve implied by the model, through a calibration against vanilla options. We can see it is again quite different. If we were to use the true replication based forward variance curve, we would effectively attempt to fit far away vols in the wings, which somehow seems wrong. Now if the model was able to fit everything well there would be no issue, but with 3 parameters per maturity, a choice has to be made. And the choice of the full replication does not look particularly great, as we fit exactly something that is not liquid.