Copilot vs ChatGPT on the Optimal Finite Difference Step-Size
When computing the derivative of a function by finite difference, which step size is optimal? The answer depends on the kind of difference (forward, backward or central), and the degree of the derivative (first or second typically for finance).
For the first derivative, the result is very quick to find (it’s on wikipedia). For the second derivative, it’s more challenging. The Lecture Notes of Karen Kopecky provide an answer. I wonder if Copilot or ChatGPT would find a good solution to the question:
“What is the optimal step size to compute the second derivative of a function by centered numerical differentiation?”
Here is the answer of copilot:
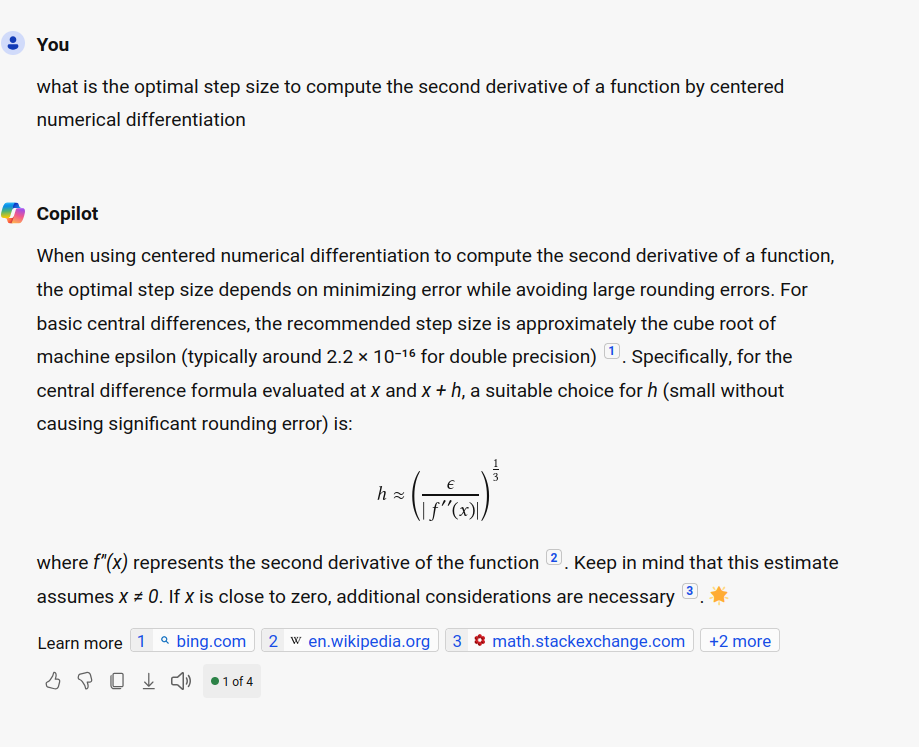


Copilot always fails to provide a valid answer. ChatGPT v4 proves to be quite impressive: it is able to reproduce some of the reasoning presented in the lecture notes.
Interestingly, with centered difference, for a given accuracy, the optimal step size is different for the first and for the second derivative. It may, at first, seem like a good idea to use a different size for each. In reality, when both the first and second derivative of the function are needed (for example the Delta and Gamma greeks of a financial product), it is rarely a good idea to use a different step size for each. Firstly, it will be slower since more the function will be evaluated at more points. Secondly, if there is a discontinuity in the function or in its derivatives, the first derivative may be estimated without going over the discontinuity while the second derivative may be estimated going over the discontinuity, leading to puzzling results.