Controlling the SABR wings with Hagan PDE
On the Wilmott forum, Pat Hagan has recently suggested to cap the equivalent local volatility in order to control the wings and better match CMS prices. It also helps making the SABR approximation better behaved as the expansion is only valid when$$ 1 + 2\frac{\rho\nu}{\alpha}y(K)+\frac{\nu^2}{\alpha^2}y^2(K) $$
is close to 1.
In the PDE approach (especially the non transformed one), it is very simple, one just needs to update the equivalent local vol as
$$\alpha K^\beta \min\left(M, \sqrt{1 + 2\frac{\rho\nu}{\alpha}y(K)+\frac{\nu^2}{\alpha^2}y^2(K)}\right)$$
While it is straightforward to include in the PDE, it is more difficult to derive a good approximation. The zero-th order behaves as expected, but the first order formula has a unnatural kink, likely because of the non differentiability due to the min function.
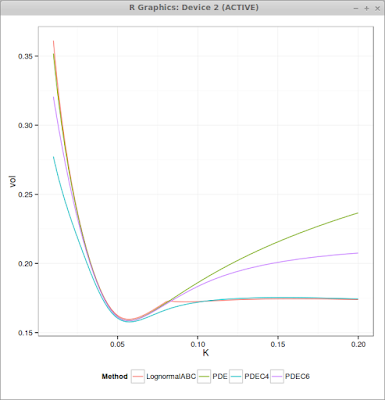
The following graphs presents the non capped PDE, the capped PDE with M=4*nu (PDEC4) and M=6*nu (PDEC6) as well as the approximation (Andersen Ratcliffe / Gatheral first order) where I have only taken care of the right wing. The SABR parameters are alpha = 0.0630, beta = 0.7, rho = -0.363, nu = 0.421, T = 10, f = 0.0439.
We can see that the higher the cap is, the closer we are to the standard SABR PDE, and the lower the cap is, the flatter are the wings.
The approximation matches well ATM (it is then equivalent to standard SABR PDE) but then has a discontinuous derivative for the K that reaches the threshold M. Far away, it matches very well again.
The approximation matches well ATM (it is then equivalent to standard SABR PDE) but then has a discontinuous derivative for the K that reaches the threshold M. Far away, it matches very well again.