Arbitrage Free SABR - Another View on Hagan Approach

Sat, Dec 14, 2013

Several months ago, I took a look at two interesting recent ways to price under SABR with no arbitrage:

• One way is due to Andreasen and Huge, where they find an equivalent local volatility expansion, and then use a one-step finite difference technique to price.
• The other way is due to Hagan himself, where he numerically solves an approximate PDE in the probability density, and then price with options by integrating on this density.

It turns out that the two ways are much closer than I first thought. Hagan PDE in the probability density is actually just the Fokker-Planck (forward) equation.

The \(\alpha D(F)\) is just the equivalent local volatility. Andreasen and Huge use nearly the same local volatility formula but without the exponential part (that is often negligible except for long maturities), directly in Dupire forward PDE:

A common derivation (for example in Gatheral book of the Dupire forward PDE is to actually use the Fokker-Planck equation in the probability density integral formula. Out of curiosity, I tried to price direcly with Dupire forward PDE and the Hagan local volatility formula, using just linear boundary conditions. Here are the results on Hagan own example:

The Local Vol direct approach overlaps the Density approach nearly exactly, except at the high strike boundary, when it comes to probability density measure or to implied volatility smile. On Andreasen and Huge data, it gives the following:

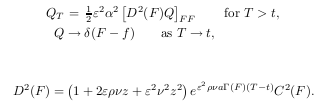
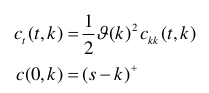
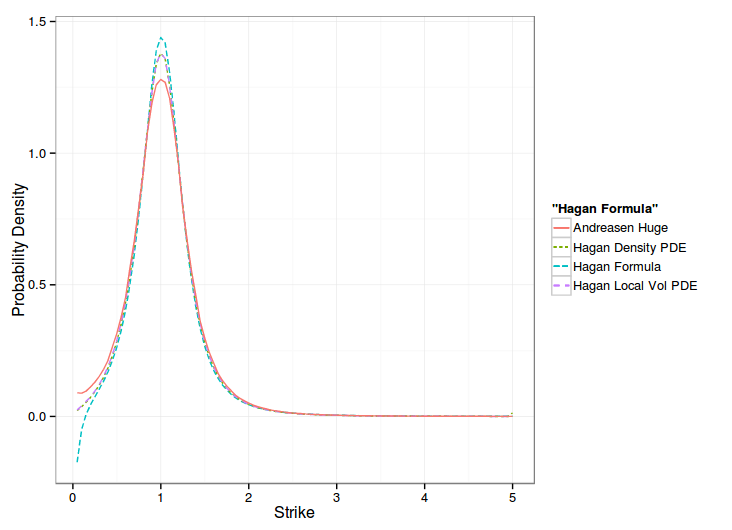
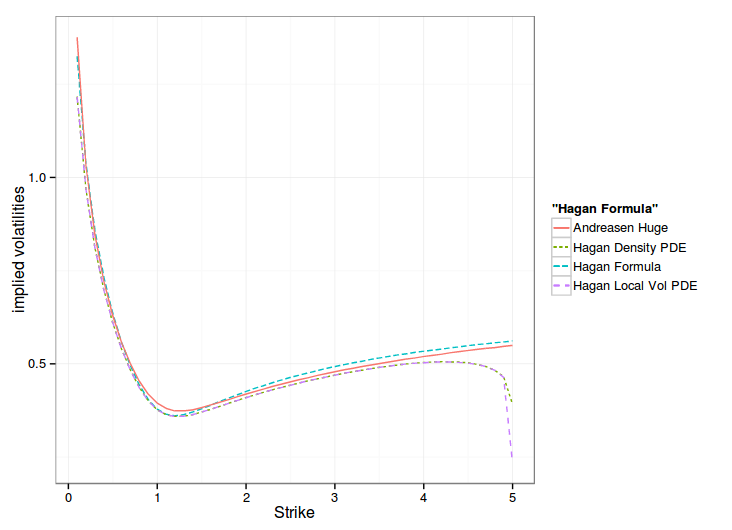
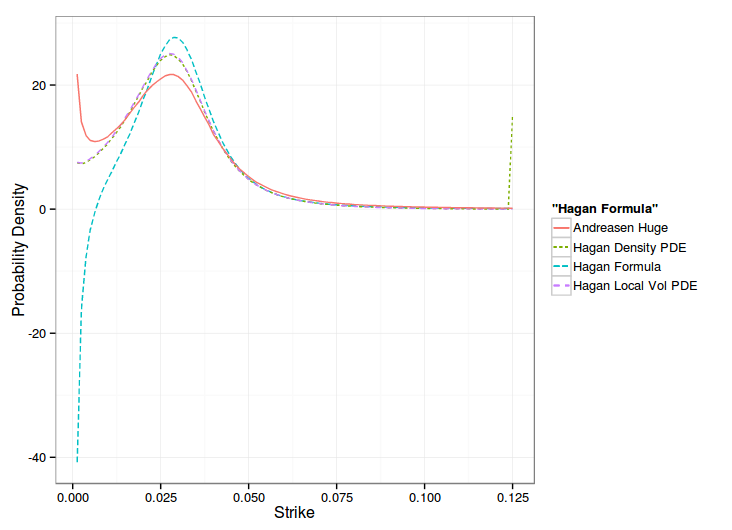
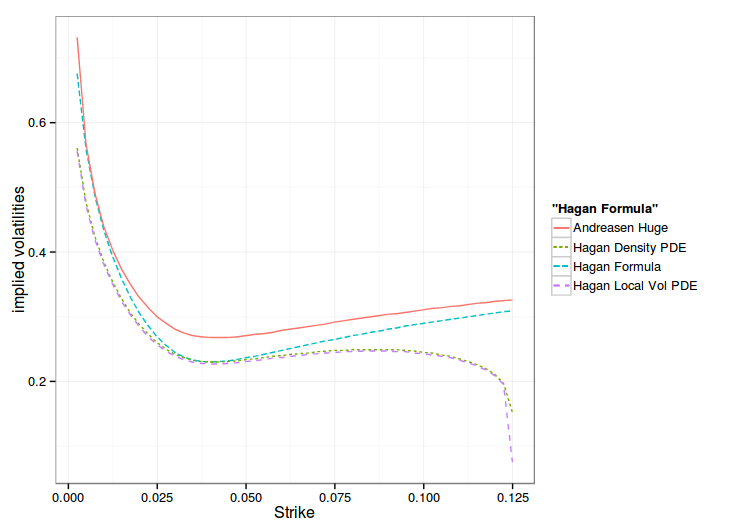
One can see that the one step method approximation gives the overall same shape of smile, but shifted, while the PDE, in local vol or density matches the Hagan formula at the money.

Hagan managed to derive a slightly more precise local volatility by going through the probability density route, and his paper formalizes his model in a clearer way: the probability density accumulates at the boundaries. But in practice, this formalism does not seem to matter. The forward Dupire way is more direct and slightly faster. This later way also allows to use alternative boundaries, like Andreasen-Huge did.

Update March 2014 - I have now a paper around this “Finite Difference Techniques for Arbitrage Free SABR”