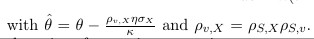Variance swaps on a foreign asset

Tue, Feb 24, 2015 There is very little information on variance swaps on a foreign asset. There can be two kinds of contracts:

• one that pays the foreign variance in a domestic currency, this is a quanto contract as the exchange rate is implicitly fixed.
• one that pays the foreign variance, multiplied by the fx rate at maturity. This is a flexo contract, and is just about buying a variance swap from a foreign bank. The price of such a contract today is very simple, just the standard variance swap price multiplied by the fx rate today (change of measure).

For quanto contracts, it's not so obvious a priori. If we consider a stochastic volatility model for the asset, the replication formula will not be applicable directly as the stochastic volatility will appear in the quanto drift correction. Furthermore, vanilla quanto option prices can not be computed simply as under Black-Scholes, a knowledge of the underlying model is necessary.

Interestingly, under the Schobel-Zhu model, it is simple to fit an analytic formula for the quanto variance swap. The standard variance swap price is:

The quanto variance swap can be priced with the same formula using a slightly different theta:

We can use it to assess the accuracy of a naive quanto option replication where we use the ATM quanto forward instead of the forward in the variance swap replication formula.


Interestingly, the  quanto forward approximation turns out to be very accurate and the correction is important. The price without correction is the price with zero correlation, and we see it can be +/-5% off in this case.

The local vol price seems a bit off, I am not sure exactly why. It could be due the discretization, the theoretical variance should be divided by (N-1) but here we divide by N where N is the number of observations. That would still lead to a skewed price but better centered around correlation 0.

It's also a bit surprising that local vol is worse than the simpler ATM quanto forward approximation: it seems that it's extracting the wrong information to do a more precise quanto correction, likely related to the shift of stochastic volatility under the domestic measure.