Upper Bounds in American Monte-Carlo
Glasserman and Yu (GY) give a relatively simple algorithm to compute lower and upper bounds of a the price of a Bermudan Option through Monte-Carlo.I always thought it was very computer intensive to produce an upper bound, and that the standard Longstaff Schwartz algorithm was quite precise already. GY algorithm is not much slower than the Longstaff-Schwartz algorithm, but what's a bit tricky is the choice of basis functions: they have to be Martingales. This is the detail I overlooked at first and I, then, could not understand why my results were so bad. I looked for a coding mistake for several hours before I figured out that my basis functions were not Martingales. Still it is possible to find good Martingales for the simple Bermudan Put option case and GY actually propose some in another paper.
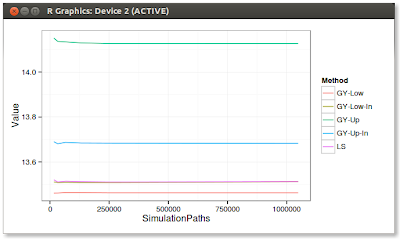
Here are some preliminary results where I compare the random number generator influence and the different methods. I include results for GY using In-the-money paths only for the regression (-In suffix) or all (no suffix).
 | |
| value using 16k training path and Sobol - GY-Low-In is very close to LS. |
 |
| error using 16k training path - a high number of simulations not that useful |
 |
| error using 1m simulation paths - GY basis functions require less training than LS |
One can see the the upper bound is not that precise compared to the lower bound estimate, and that using only in the money paths makes a big difference. GY regression is good with only 1k paths, LS requires 10x more.
Surprisingly, I noticed that the Brownian bridge variance reduction applied to Sobol was increasing the GY low estimate, so as to make it sometimes slightly higher than Longstaff-Schwartz price.