Smart Initial Guess for Schobel-Zhu
With a small time expansion, it is easy to derive a reasonable initial guess, without resorting to some global minimizer.
Like Forde did for Heston, one can find the 5 Schobel-Zhu parameters through 5 points at coordinates (0,0), (x0,t1), (-x0,t1), (x0,t2), (-x0,t2), where x0 is a chosen the log-moneyness, for example, 0.1 and t1, t2 relatively short expiries (for example, 0.1, 0.25).
We can truncate the small time expansion so that the polynomial in (x,t) is fully captured by those 5 points. In practice, I have noticed that using a more refined expansion with more terms resulted not only in more complex formulas to lookup the original stochastic volatility parameters, but also in an increased error, because of the redundancy of parameters in the polynomial expansion. My previous Schobel-Zhu expansion becomes just:
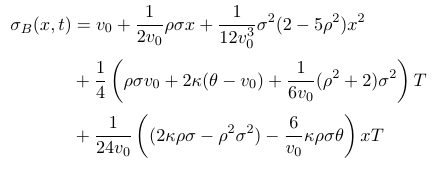
In practice, I have found that the procedure works rather well.
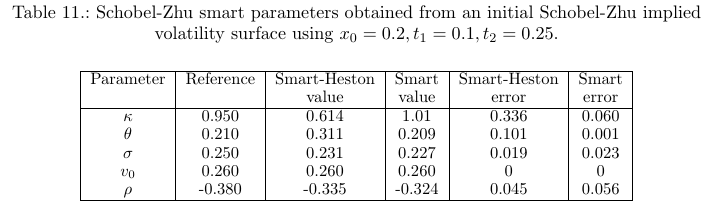
On some more extreme surfaces, where theta=0, the error in kappa and theta is higher. Interestingly, I received a few real world surfaces like this, where theta=0, which I found a bit puzzling. I wondered if it was because those surfaces were preprocessed with SABR, that has no mean reversion, but I could not fit those exactly with SABR.
Update March 2014 - this is now described in my paper Fourier Integration and Stochastic Volatility Calibration.