Shooting arbitrage - part II
In my previous post, I looked at de-arbitraging volatilities of options of a specific maturity with the shooting method. In reality it is not so practical. While the local volatility will be continuous at the given expiry \(T\), it won’t be so at the times \( t \lt T \) because of the interpolation or extrapolation in time. If we consider a single market expiry at time \(T\), it is standard practice to extrapolate the implied volatility flatly for \(t \lt T\), that is, \(w(y,t) = v_T(y) t\) where the variance at time \(T\) is defined as \(v_T(y)= \frac{1}{T}w(y,T)\). Plugging this into the local variance formula leads to $$\sigma^{\star 2}\left(y, t\right) = \frac{ v_T(y)}{1 - \frac{y}{v_T}\frac{\partial v_T}{\partial y} + \frac{1}{4}\left(-\frac{t^2}{4}-\frac{t}{v_T}+\frac{y^2}{v_T^2}\right)\left(\frac{\partial v_T}{\partial y}\right)^2 + \frac{t}{2}\frac{\partial^{2} v_T}{\partial y^2}}$$ for \(t\leq T\). In particular, for \(t=0\), we have $$\sigma^{\star 2}\left(y, 0\right) = \frac{ v_T(y)} {1 - \frac{y}{v_T}\frac{\partial v_T}{\partial y} + \frac{1}{4}\left(\frac{y^2}{v_T^2}\right)\left(\frac{\partial v_T}{\partial y}\right)^2}$$ But the first derivative is not continuous, and jumps at \(y=y_0\) and \(y=y_1\). The local volatility will jump as well around those points. Thus, in practice, the technique can not be used for pricing under local volatility.
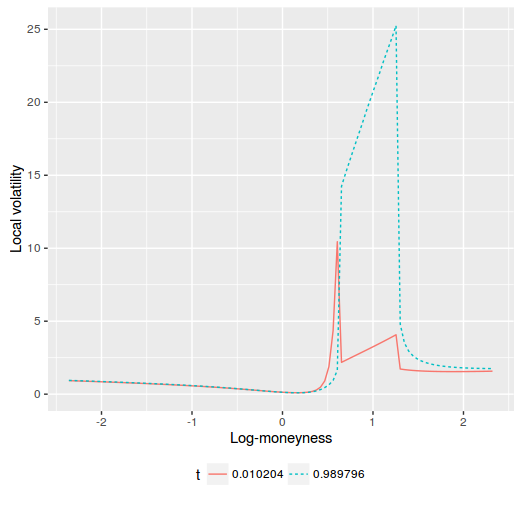
jumping local volatility on Axel Vogt example fixed by shooting
The local volatility stays very high in the original arbitrage region, very much like a capped local volatility would do. It should be then no surprise that in the equivalent implied volatility
is nearly the same as the one stemming from a capped local variance (we imply the smile from the prices of the local volatility PDE).
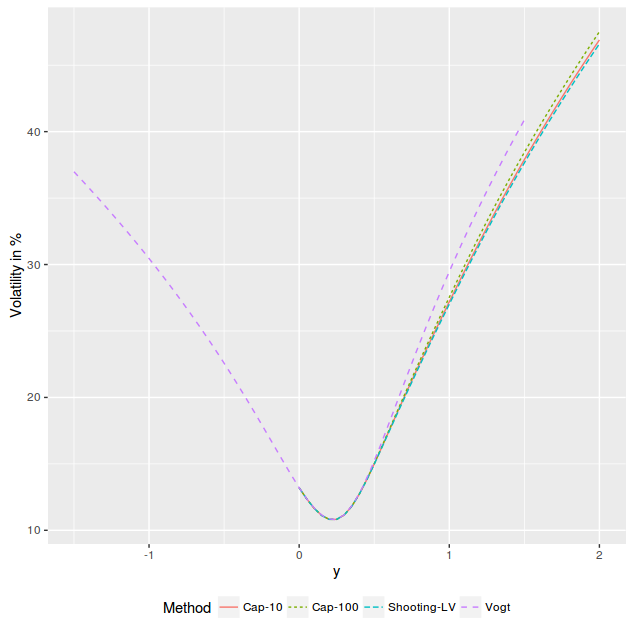
implied volatility on Axel Vogt example fixed by shooting or by capping
The discontinuity renders the shooting technique useless. The penalized spline does not have this issue as the resulting local volatility is smooth from \(t=0\) to \(t=T\).