Moore-Penrose Inverse & Gauss-Newton SABR Minimization
I have found a particularly nice initial guess to calibrate SABR. As it is quite close to the true best fit, it is tempting to use a very simple minimizer to go to the best fit. Levenberg-Marquardt works well on this problem, but can we shave off a few iterations?I firstly considered the basic Newton's method, but for least squares minimization, the Hessian (second derivatives) is needed. It's possible to obtain it, even analytically with SABR, but it's quite annoying to derive it and code it without some automatic differentiation tool. It turns out that as I experimented with the numerical Hessian, I noticed that it actually did not help convergence in our problem. Gauss-Newton converges similarly (likely because the initial guess is good), and what's great about it is that you just need the Jacobian (first derivatives). Here is a good overview of Newton, Gauss-Newton and Levenberg-Marquardt methods.
While Gauss-Newton worked on many input data, I noticed it failed also on some long maturities equity smiles. The full Newton's method did not fare better. I had to take a close look at the matrices involved to understand what was going on. It turns out that sometimes, mostly when the SABR rho parameter is close to -1, the Jacobian would be nearly rank deficient (a row close to 0), but not exactly rank deficient. So everything would appear to work, but it actually misbehaves badly.
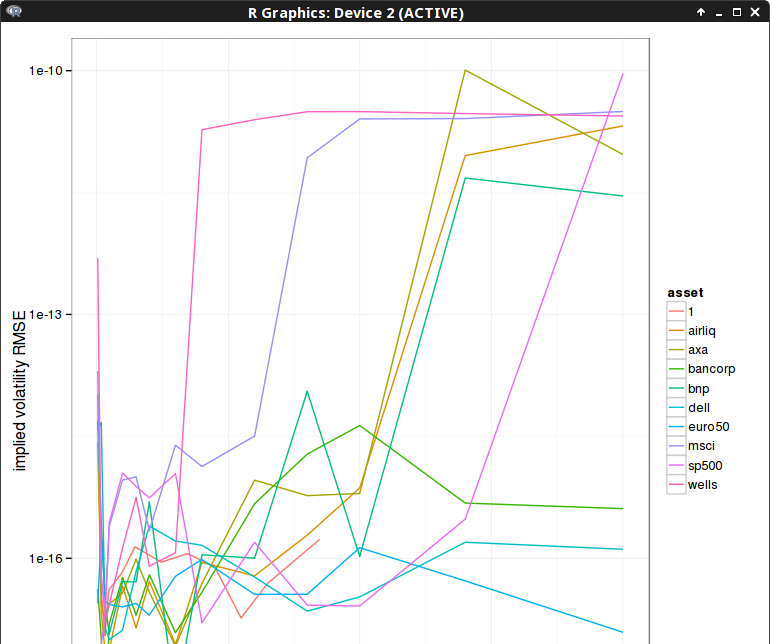
My first idea was to solve the reduced problem if a row of the Jacobian is too small, by just removing that row, and keep the previous value for the guess corresponding to that row. And this simplistic approach made the process work on all my input data. Here is the difference in RMSE compared to a highly accurate Levenberg-Marquardt minimization for 10 iterations:
Later, while reading some more material related to least square optimization, I noticed the use of the Moore-Penrose inverse in cases where a matrix is rank deficient. The Moore-Penrose inverse is defined as:
$$ M^\star = V S^\star U^T$$
where \( S^\star \) is the diagonal matrix with inverted eigenvalues and 0 if those are deemed numerically close to 0, and \(U, V\) the eigenvectors of the SVD decomposition:
$$M=U S V^T$$
It turns out to work very well, beside being simpler to code, I expected it to be more or less equivalent to the previous approach (a tiny bit slower but we don't care as we deal with small matrices, and the real slow part is the computation of the objective function and the Hessian, which is why looking at iterations is more important).
It seems to converge a little bit less quickly, likely due to the threshold criteria that I picked (1E-15).
Three iterations is actually most of the time (90%) more than enough to achieve a good accuracy (the absolute RMSE is between 1E-4 and 5E-2) as the following graph shows. The few spikes near 1E-3 represent too large errors, the rest is accurate enough compared to the absolute RMSE.
To conclude, we have seen that using the Moore-Penrose inverse in a Gauss-Newton iteration allowed the Gauss-Newton method to work on rank-deficient systems.
I am not sure how general that is, in my example, the true minimum either lies inside the region of interest, or on the border, where the system becomes deficient. Of course, this is related to a "physical" constraint, here namely rho > -1.