Making Classic Heston Integration Faster than the Cos Method
A coworker pointed to me that Andersen and Piterbarg book “Interest Rate Modeling” had a chapter on Fourier integration applied to Heston. The authors rely on the Lewis formula to price vanilla call options under Heston.
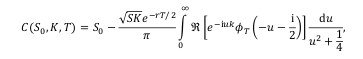
Lewis formula
More importantly, they strongly advise the use of a Black-Scholes control variate. I had read about that idea before, and actually tried it in the Cos method, but it did not improve anything for the Cos method. So I was a bit sceptical. I decided to add the control variate to my Attari code. The results were very encouraging. So I pursued on implementing the Lewis formula and their basic integration scheme (no change of variable).
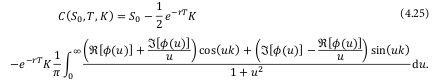
Attari formula

Carr-Madan formula (used by Lord-Kahl)
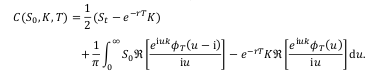
Heston formula
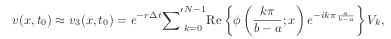
Cos formula
My impression is that the Lewis formula is not so different from the Attari formula in practice: both have a quadratic denominator, and are of similar complexity. The Lewis formula makes the Black-Scholes control variate real (the imaginary part of the characteristic function is null). The Cos formula looks quite different, but it actually is not that much different as the Vk are quadratic in the denominator as well. I still have this idea of showing how close it is to Attari in spirit.
My initial implementation of Attari relied on the log transform described by Kahl-Jaeckel to move from an infinite integration domain to a finite domain. As a result adaptive quadratures (for example based on Simpson) provide better performance/accuracy ratio than a very basic trapezoidal rule as used by Andersen and Piterbarg. If I remove the log transform and truncate the integration according by Andersen and Piterbarg criteria, pricing is faster by a factor of x2 to x3.
This is one of the slightly surprising aspect of Andersen-Piterbarg method: using a very basic integration like the Trapezoidal rule is enough. A more sophisticated integration, be it a Simpson 3/8 rule or some fancy adaptive Newton-Cotes rule does not lead to any better accuracy. The Simpson 3/8 rule won’t increase accuracy at all (although it does not cost more to compute) while the adaptive quadratures will often lead to a higher number of function evaluations or a lower overall accuracy.
Here is the accuracy on put options with a maturity of 2 years:
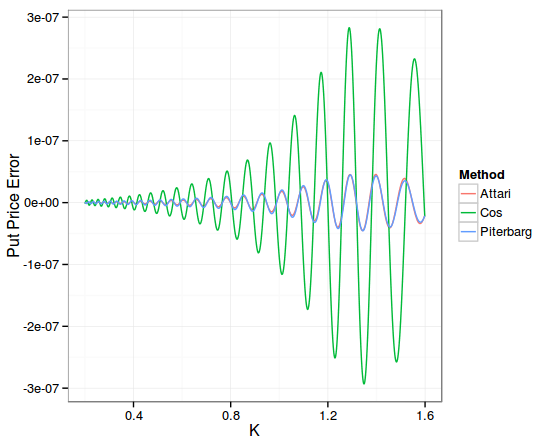
I had to push to 512 points for the Cos method and L=24 (truncation) in order to have a similar accuracy as Attari and Andersen-Piterbarg with 200 points and a control variate. For 1000 options here are the computation times (the difference is smaller for 10 options, around 30%):
| Method | Time |
|---|---|
| Attari | 0.023s |
| Andersen-Piterbarg | 0.024s |
| Cos | 0.05s |
Here is the accuracy on put options with a maturity of 2 days:
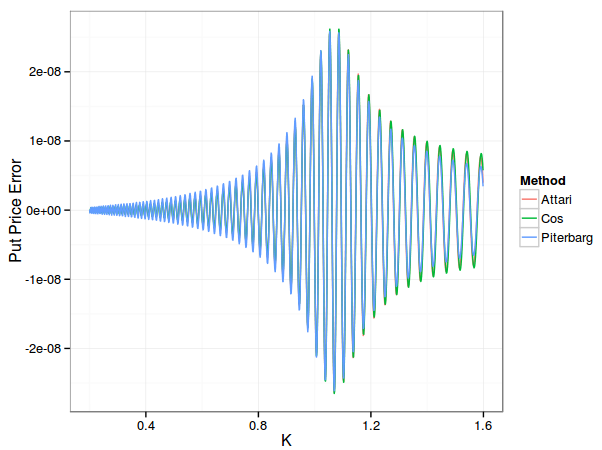
All methods used 200 points. The error is nearly the same for all. And the Cos method takes now only 0.02s. The results are similar with a maturity of 2 weeks.
Conclusion
The Cos method performs less well on longer maturities. Attari or Lewis formula with control variate and caching of the characteristic function are particularly attractive, especially with the simple Andersen-Piterbarg integration.