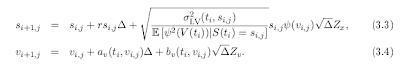Local Stochastic Volatility with Monte-Carlo
I always imagined local stochastic volatility to be complicated, and thought it would be very slow to calibrate.After reading a bit about it, I noticed that the calibration phase could just consist in calibrating independently a Dupire local volatility model and a stochastic volatility model the usual way.
One can then choose to compute on the fly the local volatility component (not equal the Dupire one, but including the stochastic adjustment) in the Monte-Carlo simulation to price a product.
There are two relatively simple algorithms that are remarkably similar, one by Guyon and Henry-Labordère in "The Smile Calibration Problem Solved":
And one from Van der Stoep, Grzelak & Oosterlee "The Heston Stochastic-Local Volatility Model: Efficient Monte Carlo Simulation":
In the particle method, the delta function is a regularizing kernel approximating the Dirac function. If we use the notation of the second paper, we have a = psi.
The methods are extremely similar, the evaluation of the expectation is slightly different, but even that is not very different. The disadvantage is that all paths are needed at each time step. As a payoff is evaluated over one full path, this is quite memory intensive.