Least Squares Spline for Volatility Interpolation
I am experimenting a bit with least squares splines. Existing algorithms (for example from the NSWC Fortran library) usually work with B-splines, a relatively simple explanation of how it works is given in this paper (I think this is how De Boor coded it in the NSWC library). Interestingly there is an equivalent formulation in terms of standard cubic splines, although it seems that the pseudo code on that paper has errors.
Least squares splines give a very good fit for option implied volatilities with only a few parameters. In theory, the number of parameters is N+2 where N is the number of interpolation points. I tried on some of my AAPL 1 month option chain, with only 3 points (so 2 splines or 5 free parameters).
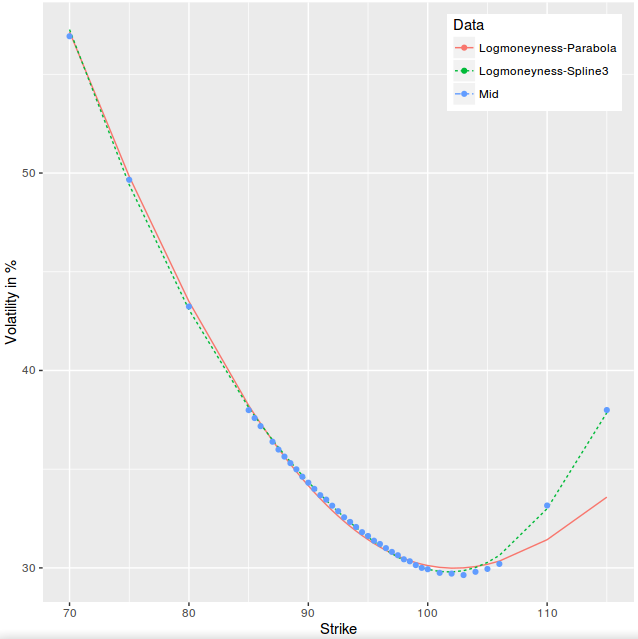
least squares spline on 1m AAPL options.
It would be interesting to add the natural constraints so that it can be linearly extrapolated. Maybe for next time.