Andreasen-Huge interpolation - Don't stay flat
Jesper Andreasen and Brian Huge propose an arbitrage-free interpolation method based on a single-step forward Dupire PDE solution in their paper Volatility interpolation. To do so, they consider a piecewise constant representation of the local volatility in maturity time and strike where the number of constants matches the number of market option prices.
An interesting example that shows some limits to the technique as described in Jesper Andreasen and Brian Huge paper comes from
Nabil Kahale paper on an arbitrage-free interpolation of volatilities.
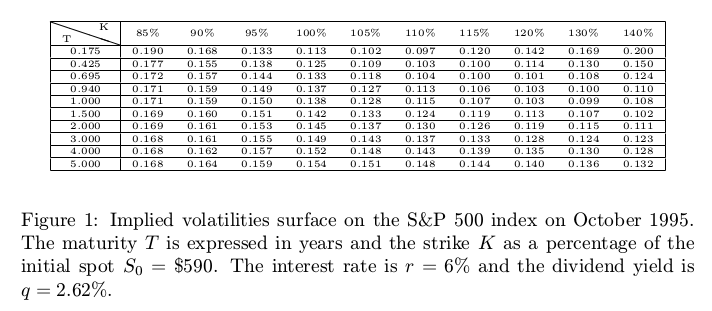
option volatilities for the SPX500 in October 1995.
Yes, the data is quite old, and as a result, not of so great quality. But it will well illustrate the issue.
The calibration of the piecewise constant volatilities on a uniform grid of 200 points (on the log-transformed problem) leads to a perfect fit:
the market vols are exactly reproduced by the following piecewise constant vols:
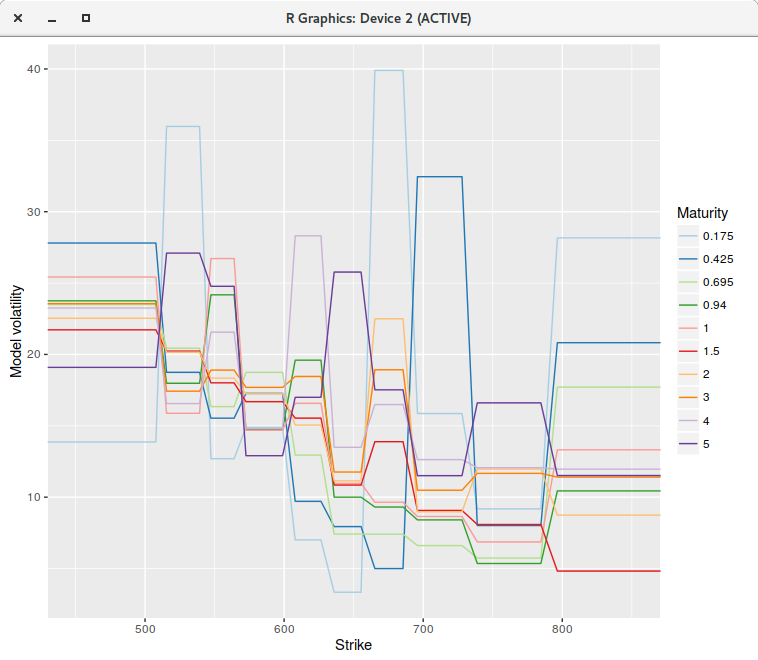
piecewise constant model on a grid of 200 points.
However, if we increase the number of points to 400 or even much more (to 2000 for example), the fit is not perfect anymore, and
some of the piecewise constant vols explode (for the first two maturities), even though there is no arbitrage in the market option prices.
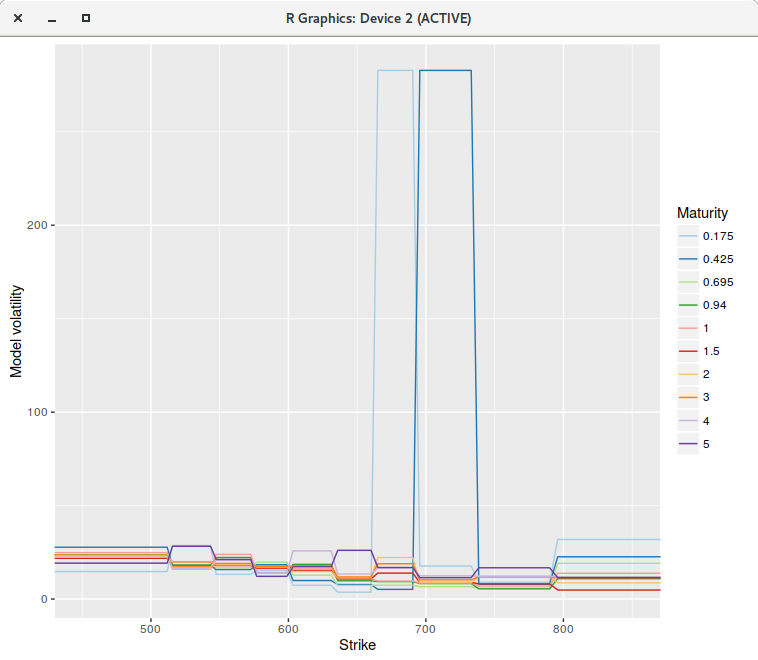
piecewise constant model on a grid of 400 points.
The single step continuous model can not represent the market implied volatilities, while for some reason, the discrete model with 200 points can. Note that the model vols were capped, otherwise they would explode even higher.
If instead of using a piecewise constant representation, we consider a continuous piecewise linear interpolation
(a linear spline with flat extrapolation), where each node falls on the grid point closest market strike, the calibration
becomes stable regardless of the number of grid points.
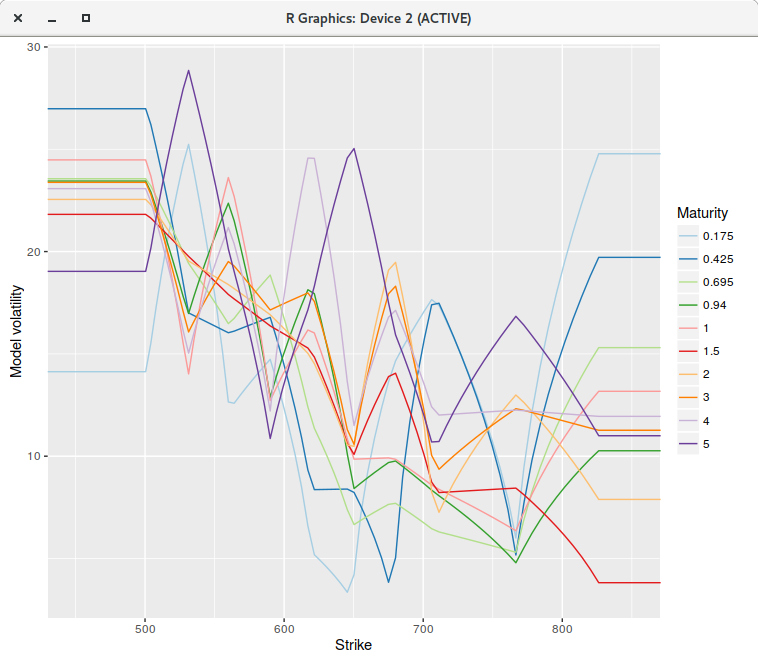
piecewise linear model on a grid of 400 points.
The RMSE is back to be close to machine epsilon. As a side effect the Levenberg-Marquardt minimization takes much less iterations to converge, either with 200 or 400 points when compared to the piecewise constant model, likely because the objective function derivatives are smoother. In the most favorable case for the piecewise constant model, the minimization with the linear model requires about 40% less iterations.
We could also interpolate with a cubic spline, as long as we make sure that the volatility does not go below zero, for example by imposing a limit on the derivative values.
Overall, this raises questions on the interest of the numerically much more complex continuous time version of the piecewise-constant model as described in Filling the gaps by Alex Lipton and Artur Sepp: a piecewise constant representation is too restrictive.