Dearbitraging a weak smile on SVI with Damghani's method
Yesterday, I wrote about some calendar spread arbitrages with SVI. Today I am looking at the famous example of butterfly spread arbitrage from Axel Vogt. $$(a, b, m, \rho, \sigma) = (−0.0410, 0.1331, 0.3586, 0.3060, 0.4153)$$ The parameters obey the weak no-arbitrage constraint of Gatheral, and yet produce a negative density, or equivalently, a negative denominator in the local variance Dupire formula. Those parameters are mentioned in Jim Gatheral and Antoine Jacquier paper on arbitrage free SVI volatility surfaces and also in Damghani’s paper dearbitraging a weak smile.
Gatheral proposes to adjust just two of the parameters (corresponding to call wing and minimum variance) and run an optimizer with a large penalty on arbitrage to find the best-fit SVI parameters. The arbitrage can be easily detected by just computing the local variance denominator, which is not much more costly than computing the implied variance (the analytical derivatives come almost for free):
It is also possible include this penalty directly in the Nelder-Mead minimization of Zeliade’s quasi explicit calibration. In this case, all the parameters will be optimized. It is also not much slower than the more classic minimization without penalty. While it results a much lower RMSE, the solution might not be as visually pleasing as Gatheral’s one.
I was curious to see what Damghani’s technique would produce on this same example. Instead of doing the minimization with the full denominator evaluation, Damghani uses a simpler no-arbitrage necessary constraint on the first derivative:
Now, it seems twisted to not enforce directly the real no arbitrage constraint in the minimization, which is actually not much more complex to evaluate, and to instead rely on some weak condition, that we make stronger by steps.
There would be no loop over the minimization needed. Does this produce any good result?
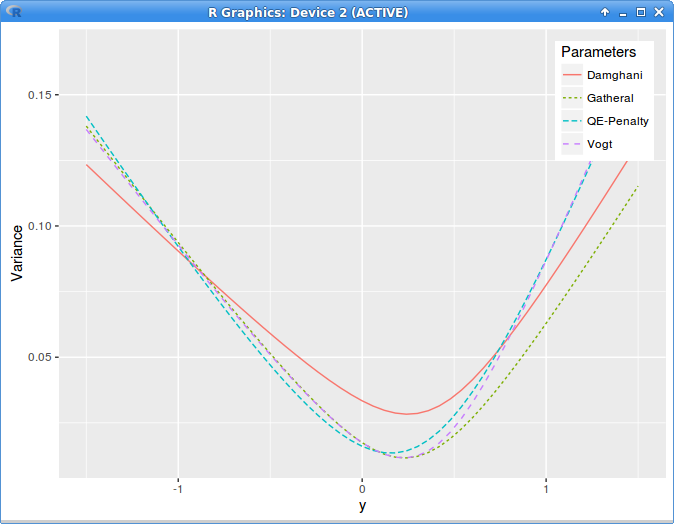
implied variance with Axel Vogt SVI parameters
The graph is clear, the technique produces crap. This is the local variance denominator:
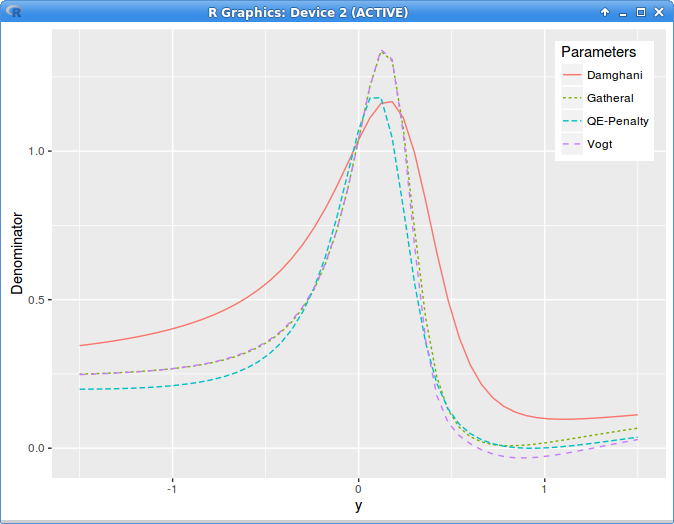
local variance denominator g with Axel Vogt SVI parameters
Maybe I misunderstood something big in this paper, but so far it was just a waste of time.