C2 Arbitrage Free Interpolation with Tension Splines
In a previous post, I have explored the arbitrage free wiggles in the volatility surface that P. Jaeckel found in his paper. I showed that interpolating in log prices instead of prices was enough to remove the wiggles, but then, it appears that the interpolation is not guaranteed to be arbitrage free, even though it often is. On another example from P. Jaeckel paper, that I reproduced inaccurately but well enough, it is not.
Using a Harmonic spline instead of a regular cubic spline seems to be enough to make the interpolation arbitrage free in practice (although not in theory as log-prices are not convex), but it is only C1.
One can use a tension spline instead. There is an algorithm from Pruess that updates the tension parameters so as to make the interpolation monotone and convex. It can be tweaked to ensure that the interpolation follows: $$f’^2 + f’’ \geq 0$$
This condition makes the interpolation on the log prices arbitrage free. As a first draft experiment, I just ensured numerically that the condition was valid, the resulting algorithm was fast enough and worked reasonably well.
Here is how the normalized density looks like with a simple harmonic spline on the call prices, a cubic spline in the logarithm of call prices, and an optimized tension spline in the logarithm of call prices.
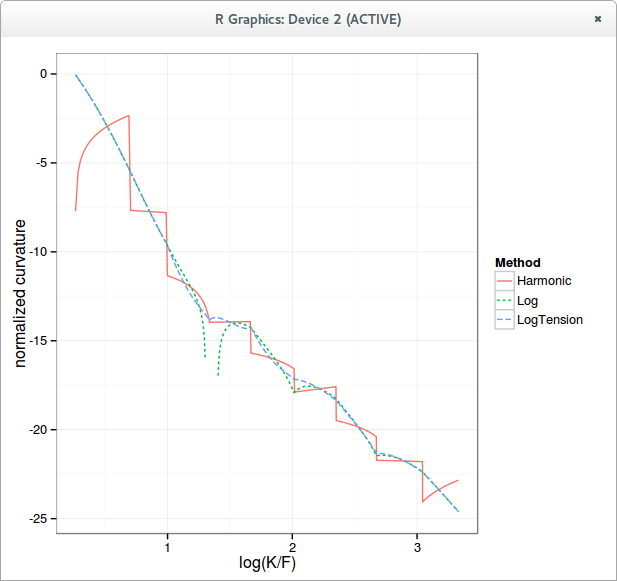
logarithm of the curvature
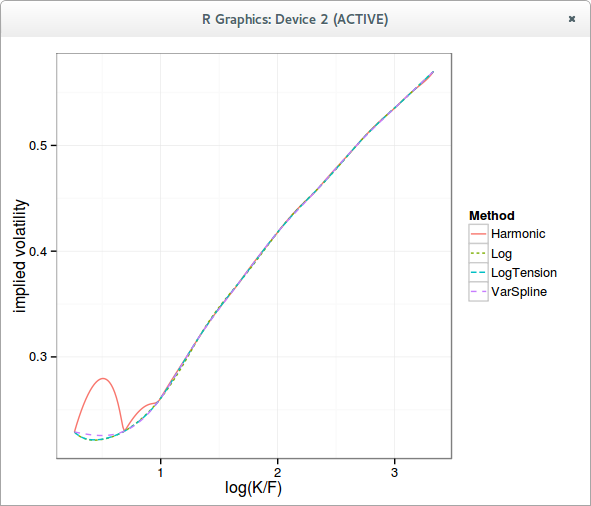
The implied volatility curve is very close to a more classic cubic spline interpolation on the implied variance.Of course, the same kind of algorithm can be applied directly to the variance with a slightly different numerical test to ensure it is arbitrage-free, it might however be easier to find a more robust and more clever algorithm in the log prices.