Arbitrage Free Wiggles

Mon, Mar 3, 2014 Peter Jaeckel, in a recent paper (pdf), shows that something that sounds like a reasonable arbitrage free interpolation can produce wiggles in the implied volatility slice.

The interpolation in question is using some convexity preserving spline on call and put option prices directly and in strike, assuming those input prices are arbitrage free. This is very similar to Kahale interpolation (pdf).

It seemed too crazy for me so I had to try out his example. And using a harmonic spline, it does produce arbitrage free wiggles.

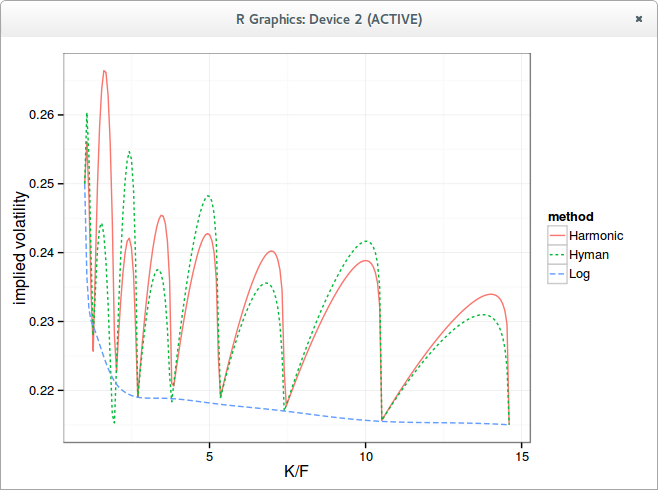Wiggles in the implied volatility

If we look at the probability density (the curvature), the Harmonic spline maintains a positive density, nearly piecewise flat in log scale, while Hyman, because it preserves only monotonicity, has some negative density which are cut out from the graph.

Probability Density

In reality, if we look at the interpolation of prices in log scale, one can see that splines won't behave as expected at first on small numbers: they will give a much higher weight to the high values, producing something like a piecewise linear interpolation.

In reality, what one really wants for such data is to just interpolate the log prices with a spline, not the prices. This is the curve named "Log" in the graphs, where a simple cubic spline is used on the log prices, and fed to exp after interpolation.

Now it sounds like a reasonable arbitrage free interpolation would be to interpolate the discrete density log linearly, in a similar spirit as Hagan-West yield curve interpolation (pdf).

In general, if you interpolate very small numbers with a spline, you probably are doing something wrong.