Arbitrage free SABR with negative rates - alternative to shifted SABR

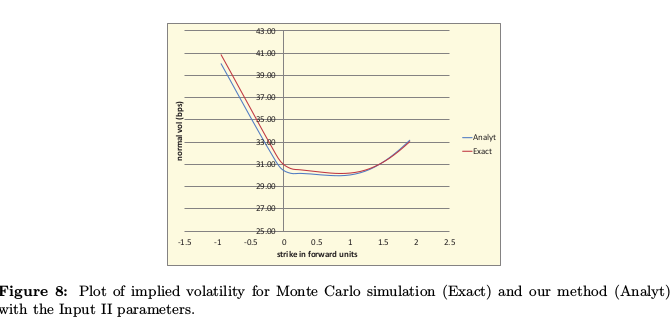
Wed, Mar 11, 2015 Antonov et al. present an interesting view on SABR with negative rates: instead of relying on a shifted SABR to allow negative rates up to a somewhat arbitrary shift, they modify slightly the SABR model to allow negative rates directly: $$ dF_t = |F_t|^\beta v_t dW_F $$ with \\( v\_t \\) being the standard lognormal volatility process of SABR.

Furthermore they derive a clever semi-analytical approximation for this model, based on low correlation, quite close to the Monte-Carlo prices in their tests. It's however not clear if it is arbitrage-free.

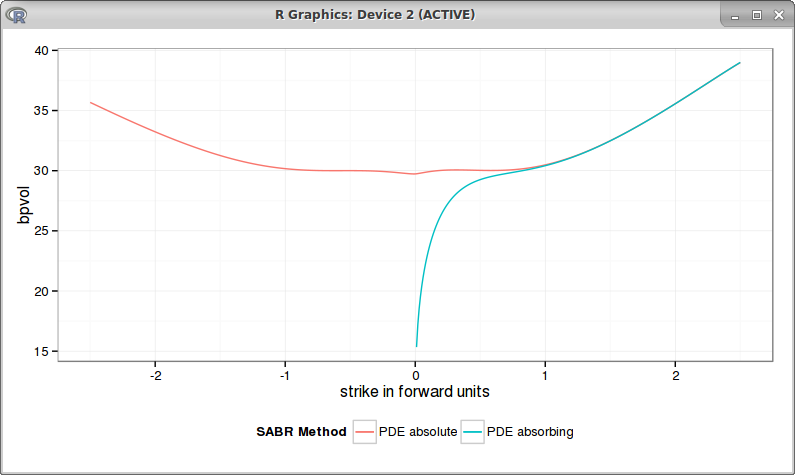
It turns out that it is easy to tweak Hagan SABR PDE approach to this "absolute SABR" model: one just needs to push the boundary \\(F\_{min}\\) far away, and to use the absolute value in C(F).

It then reproduces the same behavior as in Antonov et al. paper:

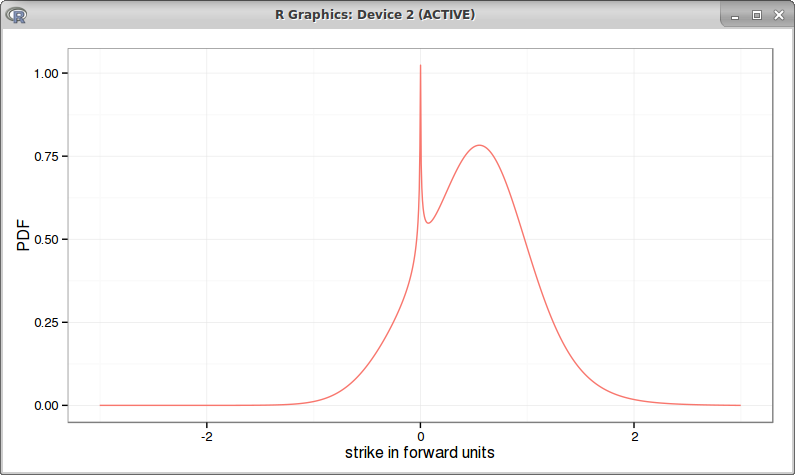"Absolute SABR" arbitrage free PDE

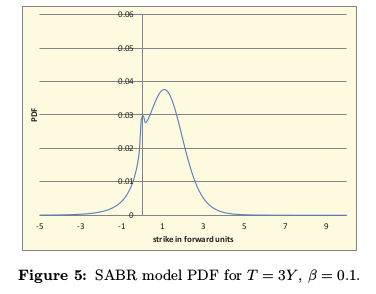Antonov et al. graph

 I obtain a higher spike, it would look much more like Antonov graph had I used a lower resolution to compute the density: the spike would be smoothed out.

Interestingly, the arbitrage free PDE will also work for high beta (larger than 0.5):

beta = 0.75

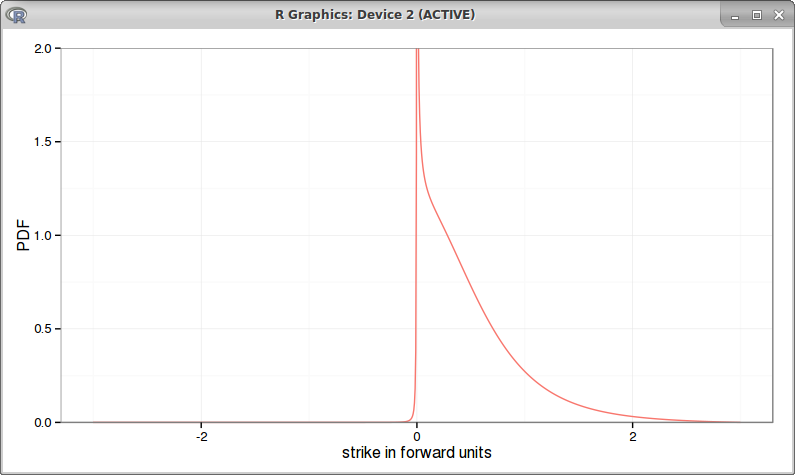It turns out to be then nearly the same as the absorbing SABR, even if prices can cross a little the 0. This is how the bpvols look like with beta = 0.75:

red = absolute SABR, blue = absorbing SABR with beta=0.75

They overlap when the strike is positive.

If we go back to Antonov et al. first example, the bpvols look a bit funny (very symmetric) with beta=0.1:

For beta=0.25 we also reproduce Antonov bpvol graph, but with a lower slope for the left wing:

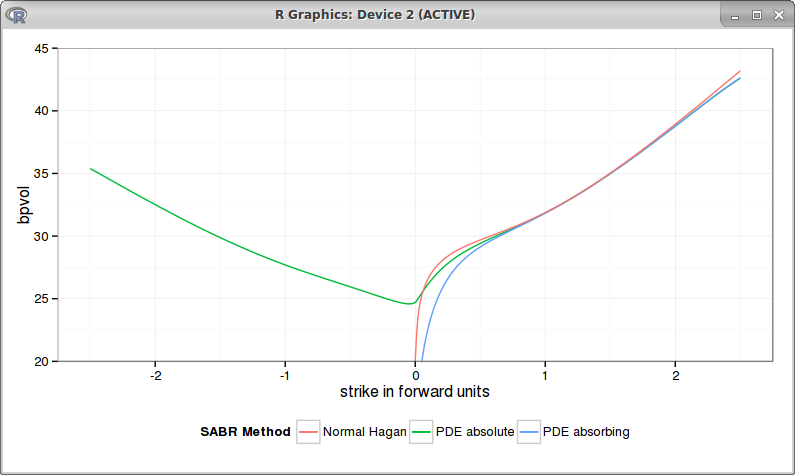bpvols with beta = 0.25

It's interesting to see that in this case, the positive strikes bp vols are closer to the normal Hagan analytic approximation (which is not arbitrage free) than to the absorbing PDE solution.

For longer maturities, the results start to be a bit different from Antonov, as Hagan PDE relies on a order 2 approximation only:

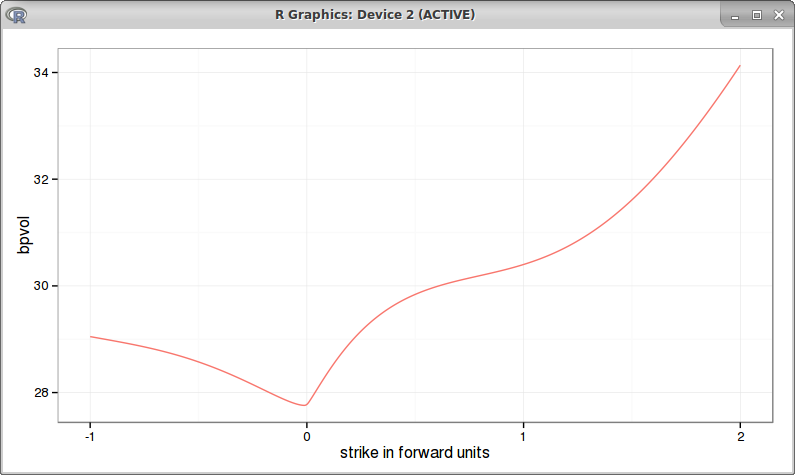absolute SABR PDE with 10y maturity

The right wing is quite similar, except when it goes towards 0, it's not as flat, the left wing is much lower.

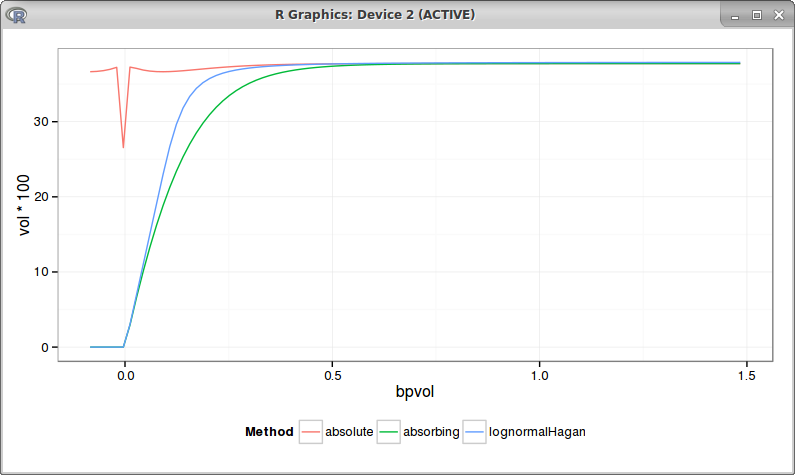
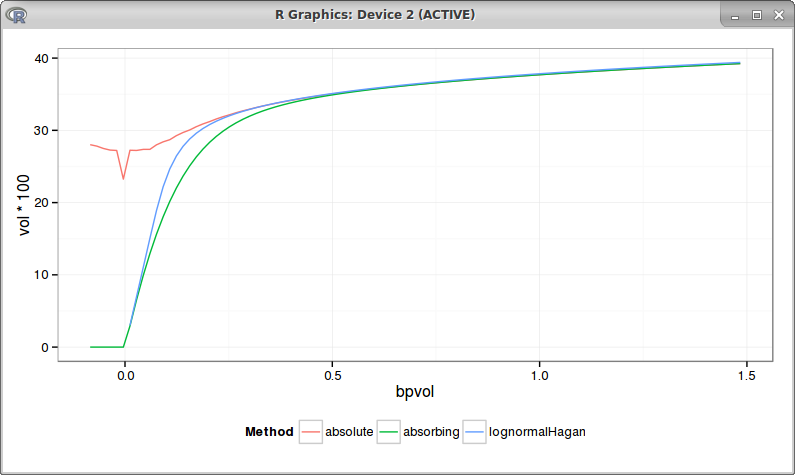
Another important aspect is to reproduce Hagan's knee, the atm vols should produce a knee like curve, as different studies show (see for example this recent Hull & White study or this other recent analysis by DeGuillaume). Using the same parameters as Hagan (beta=0, rho=0) leads to a nearly flat bpvol: no knee for the absolute SABR, curiously there is a bump at zero, possibly due to numerical difficulty with the spike in the density:
The problem is still there with beta = 0.1:



Overall, the idea of extending SABR to the full real line with the absolute value looks particularly simple, but it's not clear that it makes real financial sense.