A Small-Time Schobel-Zhu Expansion
The paper implied vol for any local stochastic vol model from Lorig et al. presents a very generic and simple formula to compute implied volatility expansions up to order-2 (there is actually an order-3 formula available in their Mathematica CDF file).
I tried it on the Schobel-Zhu stochastic volatility model. This model is an interesting alternative to Heston. I found that, in practice, the implied volatility surface fit was as good, while the simulation under the QE scheme is quite faster (and simpler) than Heston. Here is the result of applying their technique on Schobel-Zhu:
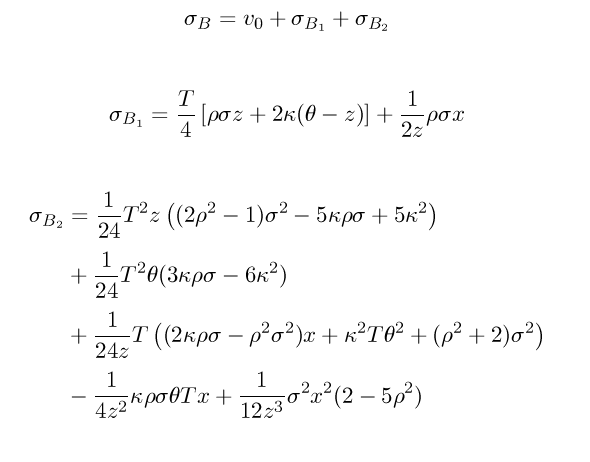
And this is how it behaves on some realistic input:
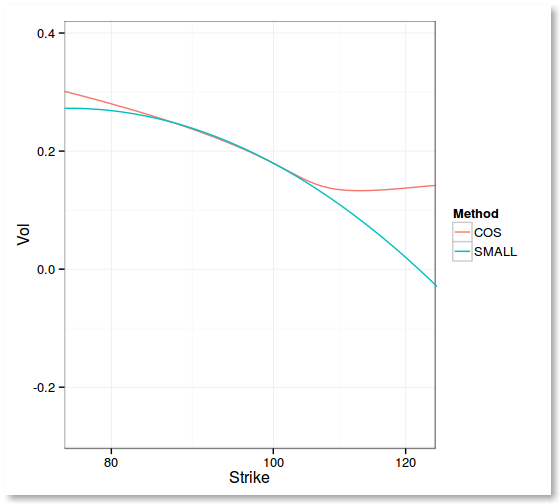
T=0.1
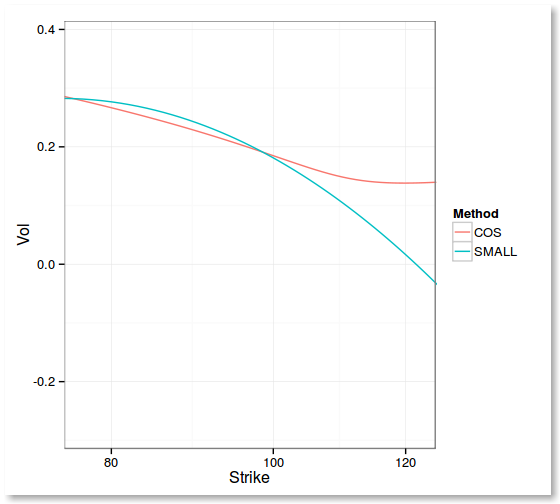
T=0.5
In practice, while not extremely good, it seems to be enough for Calibration to find an initial guess via differential evolution.
Update March 2014 - this is now described in my paper Fourier Integration and Stochastic Volatility Calibration.