A Look at Small Time Expansions for Heston
Small time expansions for Heston can be useful during the calibration of the implied volatility surface, in order to find an initial guess for a local minimizer (for example, Levenberg-Marquardt). Even if they are not so accurate, they capture the dynamic of the model parameters, and that is often enough.
In 2011, Forde et al. proposed a second order small time expansion around the money, which I found to work well for calibration. More recently, Lorig et al. proposed different expansions up to order-3 around the money. I already looked at the later in my previous post, applying the idea to Schobel-Zhu.
I noticed, however, that on some surfaces, the Lorig expansion was quickly very inaccurate (LPP1 for order-1, LPP2 for order-2, LPP3 for order-3). Those surfaces seem to be the ones were the Feller condition is largely violated. In practice, in my set of volatility surfaces for 10 different equities/indices, the best fit is always produced by Heston parameters where the Feller condition is violated.

T=0.5, Feller condition largely violated
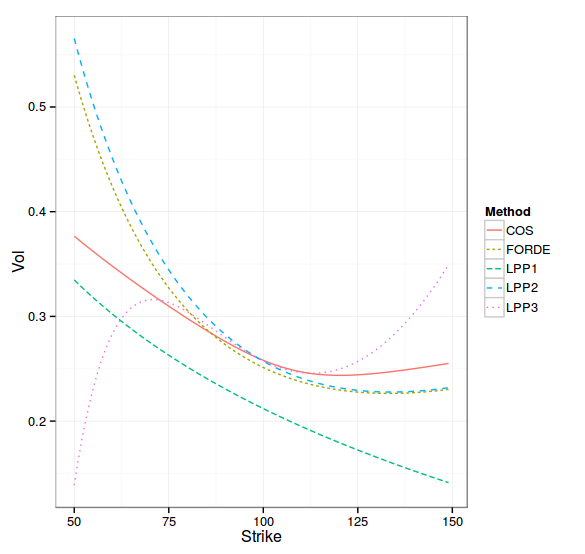
T=0.5, Feller condition slightly violated
Out of curiosity, I calibrated my surfaces feeding the order-1 approximation to the differential evolution, in order to find my initial guess, and it worked for all surfaces. The order-3 formula, even though it is more precise at the money, was actually more problematic for calibration: it failed to find a good enough initial guess in some cases, maybe because the reference data should be truncated, to possibly keep the few shortest expiries, and close to ATM strikes.