SVI and long maturities issues
On long maturities equity options, the smile is usually very much like a skew: very little curvature. This usually means that the SVI rho will be very close to -1, in a similar fashion as what can happen for the the correlation parameter of a real stochastic volatility model (Heston, SABR).
In terms of initial guess, I looked at the more usual use cases and showed that matching a parabola at the minimum variance point often leads to a decent initial guess if one has an ok estimate of the wings. We will see here that we can do also something a bit better than just a flat slice at-the-money in the case where rho is close to -1.
In general when the asymptotes lead to rho < -1, it means that we can’t compute b from the asymptotes as there is in reality only one usable asymptote, the other one having a slope of 0 (rho=-1). The right way is to just recompute b by matching the ATM slope (which can be estimated by fitting a parabola at the money). Then we can try to match the ATM curvature, there are two possibilities to simplify the problem: s » m or m » s.
Interestingly, there is some kind of discontinuity at m = 0:
- when m = 0, the at-the-money slope is just b*rho.
- when m != 0 and m » s, the at-the-money slope is b*(rho-1).
In general it is therefore a bad idea to use m=0 in the initial guess. It appears then that assuming m » s is better. However, in practice, with this choice, the curvature at the money is matched for a tiny m, even though actually the curvature explodes (sigma=5e-4) at m (so very close to the money). This produces this kind of graph:
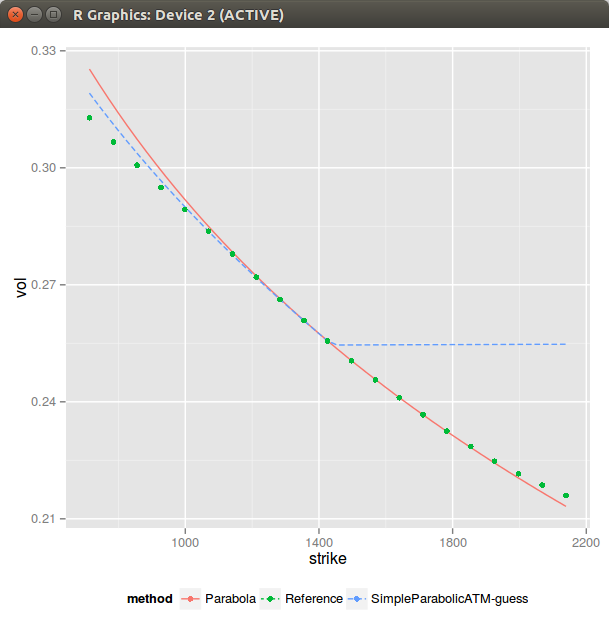
This apparently simple issue is actually a core problem with SVI. Looking back at our slopes but this time in the moneyness coordinate, the slope at m is \(b \rho\) while the slope at the money is \(b(\rho-1)\) if m != 0. If s is small, as the curvature at m is just b/s this means that our there will always be this funny shape if s is small. It seems then that the best we can do is hide it: let m > max(moneyness) and compute the sigma to match the ATM curvature. This leads to the following:
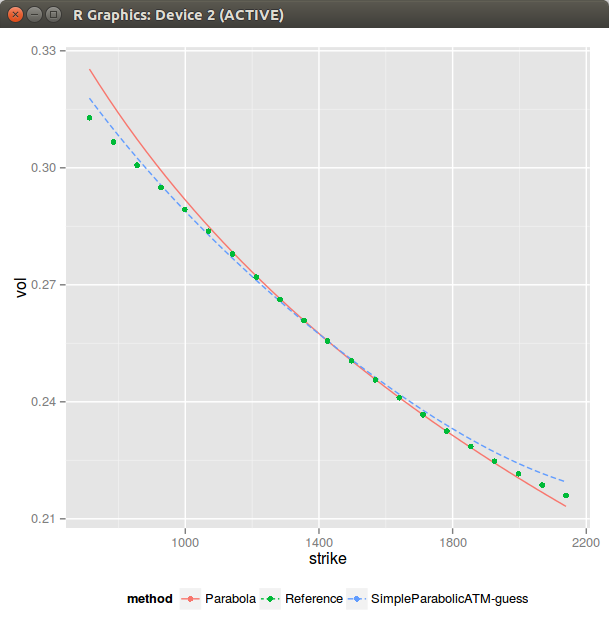
This is all good so far. Unfortunately running a minimizer on it will lead to a solution with a small s. And the bigger picture looks like this (QE is Zeliade Quasi-Explicit, Levenberg-Marquardt would give the same result):
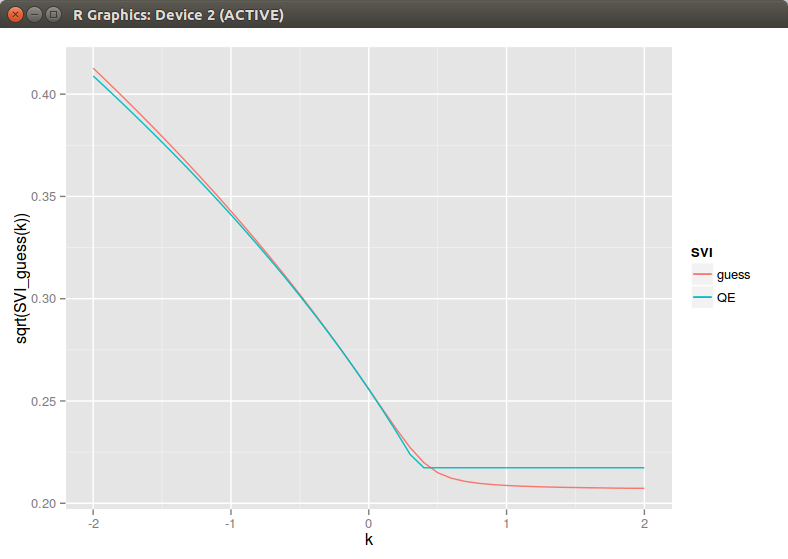
Of course a simple fix is to not let s to be too small, but how do we defined what is too small? I have found that a simple rule is too always ensure that s is increasing with the maturity supposing that we have to fit a surface. This rule has also a very nice side effect that spurious arbitrages will tend to disappear as well. On the figure above, I can bet that there is a big arbitrage at k=m for the QE result.