Square Root Crank-Nicolson

Fri, Jun 19, 2015 C. Reisinger kindly pointed out to me this paper around square root Crank-Nicolson. The idea is to apply a square root of time transformation to the PDE, and discretize the resulting PDE with Crank-Nicolson. Two reasons come to mind to try this:

• the square root transform will result in small steps initially, where the solution is potentially not so smooth, making Crank-Nicolson behave better.
•  it is the natural time of the Brownian motion.

Interestingly, it has nicer properties than what those reasons may suggest. On the Fokker-Planck density PDE, it does not oscillate under some very mild conditions and preserves density positivity at the peak.

Out of curiosity I tried it to price a one touch barrier option. Of course there is an analytical solution in my test case (Black-Scholes assumptions), but as soon as rates are assumed not constant or local volatility is used, there is no other solution than a numerical method. In the later case, finite difference methods are quite good in terms of performance vs accuracy.

The classic Crank-Nicolson gives a reasonable price, but the strong oscillations near the barrier, at every time step are not very comforting.

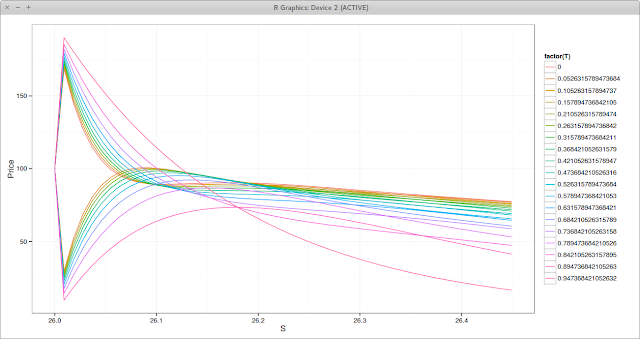Crank-Nicolson Prices near the Barrier. Each line is a different time.

Moving to square root of time removes nearly all oscillations on this problem, even with a relatively low number of time steps compared to the number of space steps.

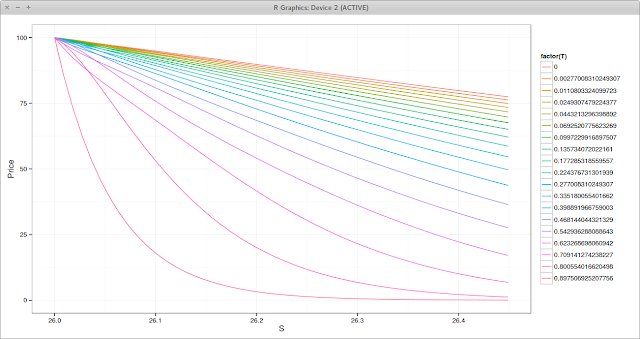Square Root Crank-Nicolson Prices near the Barrier. Each line is a different time.

We can see that the second step prices are a bit higher than the third step (the lines cross), which looks like a small numerical oscillation in time, even if there is no oscillation is space.

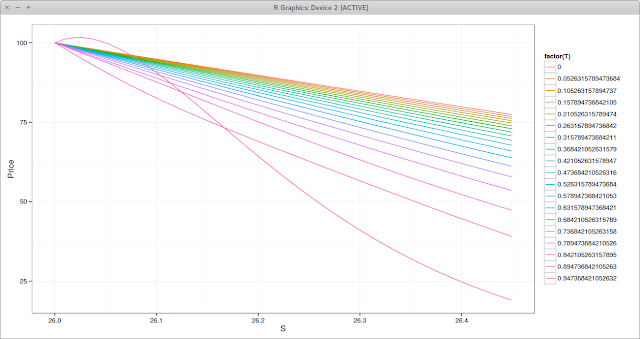TR-BDF2 Prices near the Barrier. Each line is a different time.

As a comparison, the TR-BDF2 scheme does relatively well: oscillations are removed after the second step, even with the extreme ratio of time steps vs space steps used on this example so that illustrations are clearer - Crank-Nicolson would still oscillate a lot with 10 times less space steps but we would not see oscillation on the square root Crank-Nicolson and a very mild one on TR-BDF2.

The LMG2 scheme (a local richardson extrapolation) does not oscillate at all on this problem but is the slowest:

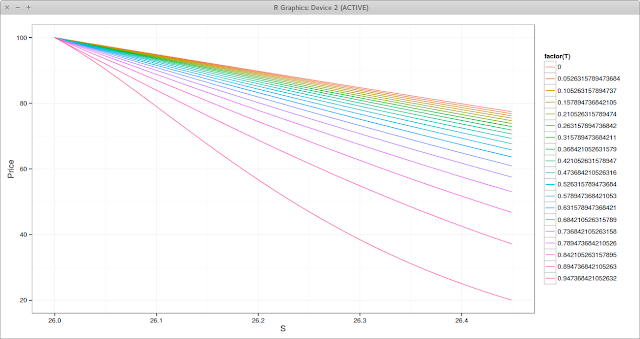LMG2 Prices near the Barrier. Each line is a different time.

The square root Crank-Nicolson is quite elegant. It can however not be applied to that many problems in practice, as often some grid times are imposed by the payoff to evaluate, for example in a case of a discrete weekly barrier. But for continuous time problems (density PDE, Vanilla, American, continuous barriers) it's quite good.

In reality, with a continuous barrier, the payoff is not discontinuous at every step, but it is only discontinuous at the first step. So Rannacher smoothing would work very well on that problem:

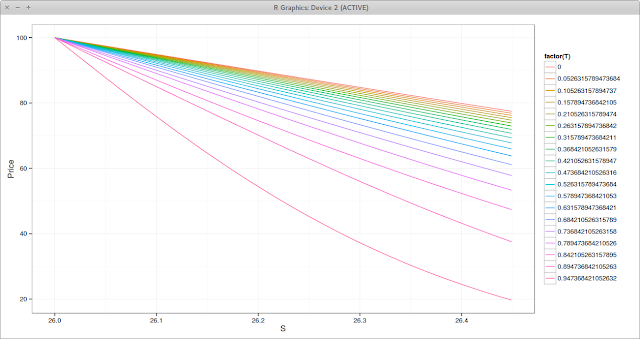Rannacher Prices near the Barrier. Each line is a different time.

The somewhat interesting payoff left for the square root Crank-Nicolson is the American.