Second Cumulant of Heston
I recently stumbled upon an error in the various papers related to the Heston Cos method regarding the second cumulant. It is used to define the boundaries of the Cos method. Letting phi be Heston characteristic function, the cumulant generating function is: $$g(u) = \log(\phi(-iu))$$
And the second cumulant is defined a: $$c_2 = g’’(0)$$Compared to a numerical implementation, the c_2 from the paper is really off in many use cases.
This is where Maxima comes useful, even if I had to simplify the results by hand. It leads to the following analytical formula: $$c_2 = \frac{v_0}{4\kappa^3}{ 4 \kappa^2 \left(1+(\rho\sigma t -1)e^{-\kappa t}\right) + \kappa \left(4\rho\sigma(e^{-\kappa t}-1)-2\sigma^2 t e^{-\kappa t}\right)+\sigma^2(1-e^{-2\kappa t}) }\\+ \frac{\theta}{8\kappa^3} { 8 \kappa^3 t - 8 \kappa^2 \left(1+ \rho\sigma t + (\rho\sigma t-1)e^{-\kappa t}\right) + 2\kappa \left( (1+2e^{-\kappa t})\sigma^2 t+8(1-e^{-\kappa t})\rho\sigma \right) \\+ \sigma^2(e^{-2\kappa t} + 4e^{-\kappa t}-5) }$$
In contrast, the paper formula was:
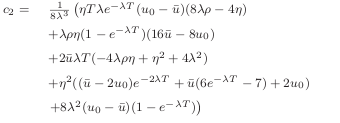
I saw this while trying to calibrate Heston on a bumped surface: the results were very different with the Cos method than with the other methods. The short maturities were mispriced, except if one pushed the truncation level L to 24 (instead of the usual 12), and as a result one would also need to significantly raise the number of points used in the Cos method. With the corrected formula, it works well with L=12.
Here is an example of failure on a call option of strike, spot 1.0 and maturity 1.0 and not-so-realistic Heston parameters $$\kappa=0.1, \theta=1.12, \sigma=1.0, v_0=0.2, \rho=-0377836$$ using 200 points:
| Formula | Value |
|---|---|
| New | 0.1640581405 |
| Paper | 0.1743425406 |
| N=30 with 10000 points | 0.1640581423 |
Update March 2014 - this is now described in my paper Fourier Integration and Stochastic Volatility Calibration.