Root finding in Lord Kahl Method to Compute Heston Call Price

Tue, Apr 9, 2013

I just tried to implement Lord Kahl algorithm to compute the Heston call price. The big difficulty of their method is to find the optimal alpha. That’s what make it work or break. The tricky part is that the function of alpha we want to minimize has multiple discontinuities (it’s periodic in some ways). This is why the authors rely on the computation of an alpha_max: bracketing is very important, otherwise your optimizer will jump the discontinuity without even noticing it, while you really want to stay in the region before the first discontinuity.

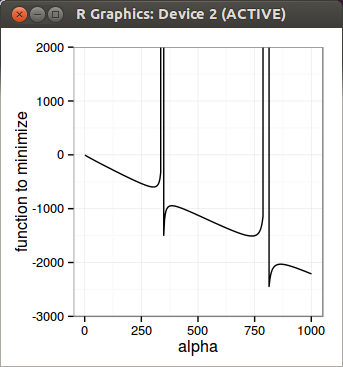
To find alpha_max, they solve a non linear differential equation, for which I would need a few more readings to really understand it. Given that the problem looked simple: if you graph the function to minimize, it seems so simple to find the first discontinuity. So I just tried to do it directly. Numerically, I was surprised it was not so simple. I did find a solution that, amazingly seems to work in all the examples of the paper, but it’s luck. I use Newton-Raphson to find the discontinuity, on a reduced function where the discontinuity really lies. I solve the inverse of the discontinuity so that I can just solve for 0. Earlier on I reduced the function too much and it did not work, this is why I believe it is not very robust. Newton-Raphson is quite simple, but also simple to understand why it breaks if it breaks, and does not need a bracketing (what I am looking for in the first place). Once I find the discontinuity, I can just use Brent on the right interval and it works well.

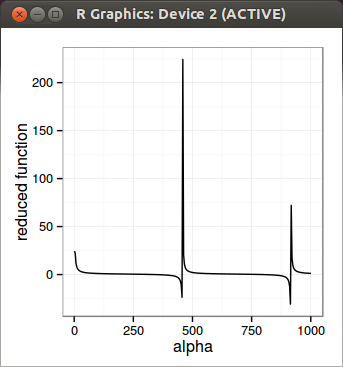
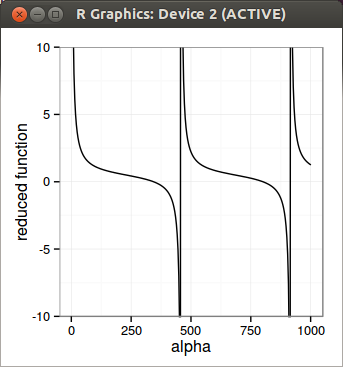
In the end, it’s neat to be able to compute option prices under machine epsilon. But in practice, it’s probably not that useful. For calibration, those options should have a very small (insignificant) weight. The only use case I found is really for graphing so that you don’t have some flat extrapolation too quickly, especially for short maturities. I was curious as well about the accuracy of some approximations of the implied volatility in the wings, to see if I could use them instead of all this machinery.

In any case I did not think that such a simple problem was so challenging numerically.

There is a part II to this article.