On the importance of accuracy for bpvol solvers
While I was playing around calibrating the arbitrage free SABR model from Hagan (using the PDE on probability density approach), I noticed a misbehavior for some short maturity smiles. I thought it was due to the PDE implementation. Actually some of it was, but the remaining large error was due to the bpvol solver.
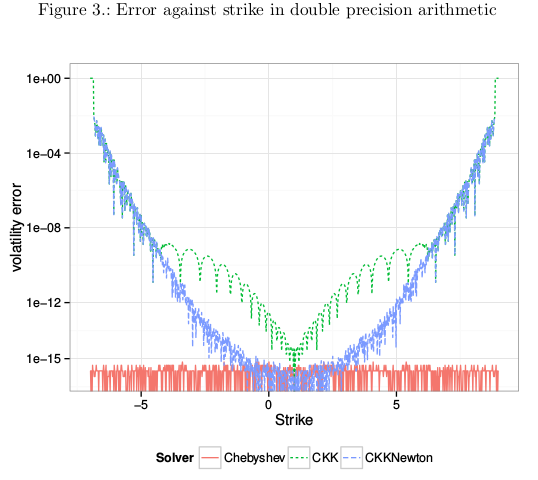
I initially took the same approach as Choi et al. in my solver, that is to work with in-the-money prices (they work with straddles) because it’s nice and convenient. I thought it was no big deal if prices lower than 1E-16 were not solved. It turns out I was wrong. Choi et al. solver has the same issue.
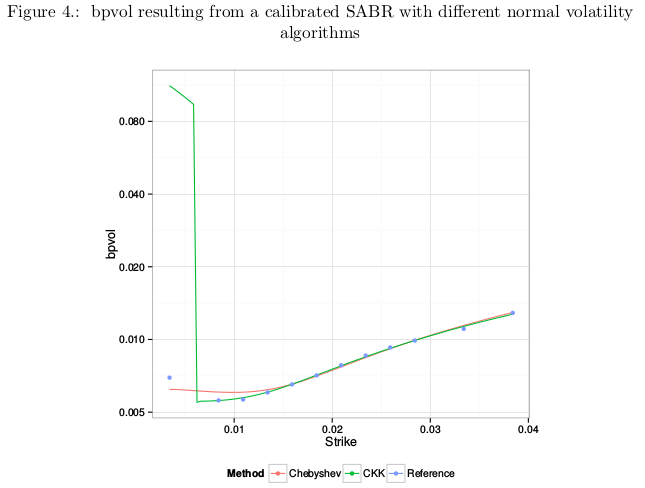
In the above figure, CKK denotes the Choi et al algorithm (similar with my old algorithm) and Chebyshev is my updated algorithm that is accurate with far out-of-the-money option. What happens is that even though the market price at the lowest strike is not very low, the price at the lowest strike stemming from the best fit smile is extremely low, and when we want to invert it, CKK produces a large error due to lack of representation of numbers near 1.0 as it uses indirectly the in-the-money price. That’s where it introduces a particularly big error in this case.
I have updated my solver since, to work with out-of-the-money option prices as well, and have near machine accuracy on the whole range. I also reduced the number of Chebyshev polynomials used in the process. All the details are in my updated paper at http://papers.ssrn.com/abstract=2420757