Matching Hagan PDE SABR with the one-step Andreasen-Huge SABR
I looked nearly two years ago already at the arbitrage free SABR of Andreasen-Huge in comparison to the arbitrage free PDE of Hagan and showed how close the ideas were: Andreasen-Huge relies on the normal Dupire forward PDE using a slightly simpler local vol (no time dependent exponential term) while Hagan works directly on the Fokker-Planck PDE (you can think of it as the Dupire Forward PDE for the density) and uses an expansion of same order as the original SABR formula (which leads to an additional exponential term in the local volatility).
One clever idea from Andreasen-Huge is the use of a single step. It turns out that their idea is not completely new. Daniel Duffy sent me some old papers from Shishkin around fitted schemes (here is one). This is very much the same thing, except Shishkin concern is about a good handling of discontinuity in the initial condition, and therefore makes the association step function => cumulative density to fit the diffusion parameter. Andreasen-Huge work directly with the call prices as this is what they solve.
One drawback of Andreasen-Huge one step method is the inability to match the standard SABR smile: the parameters don’t have exactly the same meaning. It turns out that by just shifting proportionally the local volatility by a constant factor, Andreasen Huge matches Hagan PDE vols quite closely.
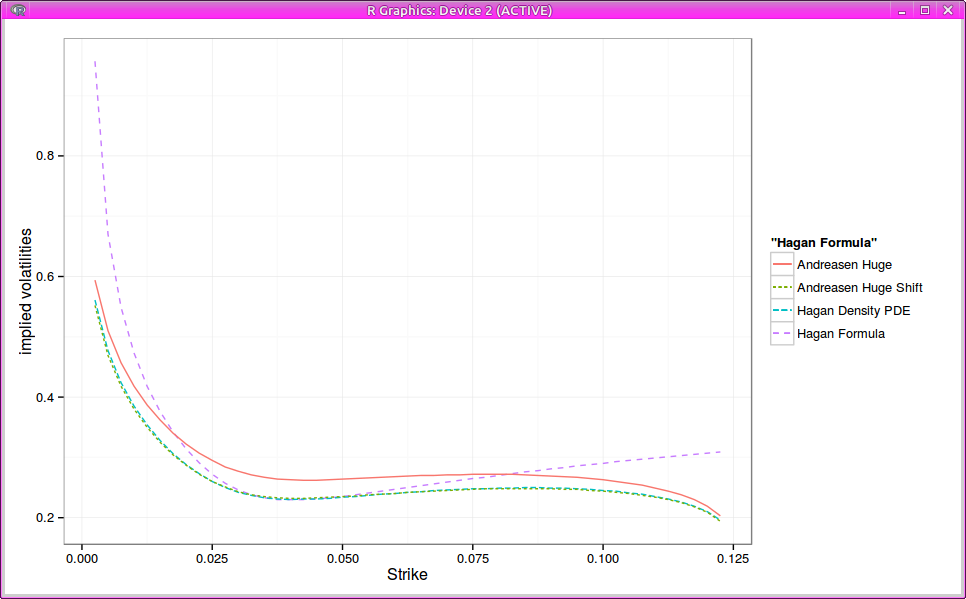
Implied Black volatilities
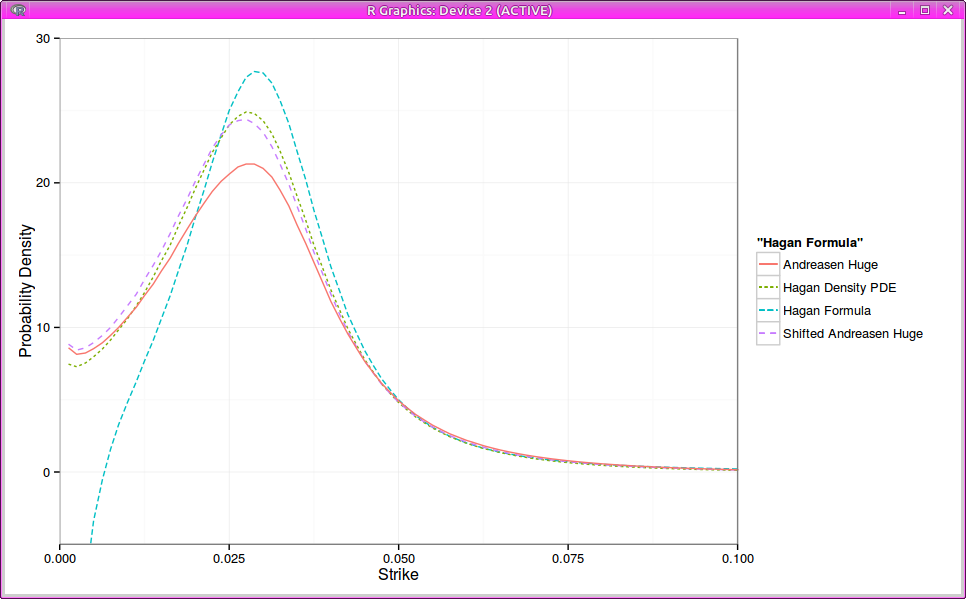
Probability density
While this is interesting in itself, it’s still not so simple to backup this factor without solving for it (and then the method looses appeal).