Heston vs SABR slice by slice fit
Some people use Heston to fit one slice of a volatility surface. In this case, some parameters are clearly redundant. Still, I was wondering how it fared against SABR, which is always used to fit a slice. And what about Schobel-Zhu?
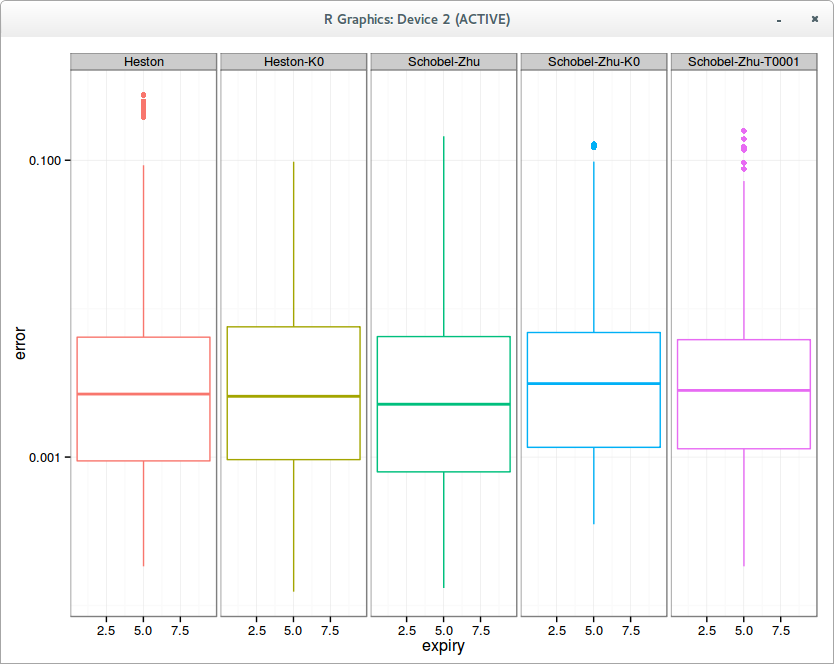
Aggregated error in fit per slice on 10 surfaces
With Heston, the calibration is actually slightly better with kappa=0, that is, without mean reversion, because the global optimization is easier and the mean reversion is fully redundant. It’s still quite remarkable that 3 parameters result in a fit as good as 5 parameters.
This is however not the case for Schobel-Zhu, where each “redundant parameter” seem to make a slight difference in the quality of calibration. kappa = 0 deteriorate a little bit the fit (the mean error is clearly higher), and theta near 0 (so calibrating 4 parameters) is also a little worse (although better than kappa = 0). Also interestingly, the five parameters Schobel-Zhu fit is slightly better than Heston, but not so when one reduce the number of free parameters.
So what about Heston vs SABR. It is interesting to consider the case of general Beta and Beta=1: it turns out that as confirmed for equities, beta=1 is actually a better choice.
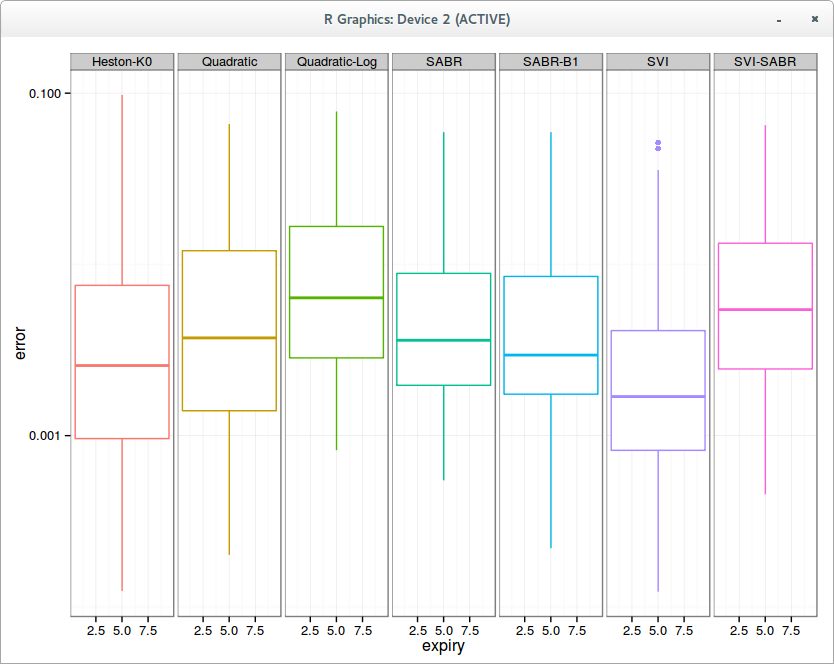
Aggregated error in fit per slice on 10 surfaces
Overall on my 10 surfaces composed each of around 10 slices, an admittedly small sample, Heston (without mean-reversion) fit is a little bit better than SABR. Also the SVI-SABR idea from Gatheral is not great: the fit is clearly worse than SABR with Beta=1 and even worse than a simple quadratic. Of course the best overall fit is achieved with the classic SVI, because it has 6 parameters while the others have only 3.
All the calibrations so far were done slice by slice independently, using levenberg marquardt on an initial guess found by differential evolution. Some people advocate for speed or stability of parameters reasons the idea of calibrating each slice using the previous slice as initial guess with a local optimizer like levenberg marquardt, in a bootstrapping fashion.

The results can be quite different, especially for SVI, which then becomes the worst, even worse than SVI-SABR, which is actually a subset of SVI with fewer parameters. How can this be?
This is because as the number of parameters increases, the first slices optimizations have a disproportionate influence, and finding the real minimum is much more difficult, even with differential evolution for the first slice. It’s easy to picture that you’ll have much more chances to get stuck in some local minimum. It’s interesting to note that the real stochastic volatility models are actually better behaved in this regard, but I am not so sure that this kind of calibration is such a great idea in general.
In practice, the SVI parameters fitted independently evolve in a given surface on each slice in a smooth manner, mostly monotonically. It’s just that to go from one set on one slice to the other on the next slice, you might have to do something more than a local optimization.