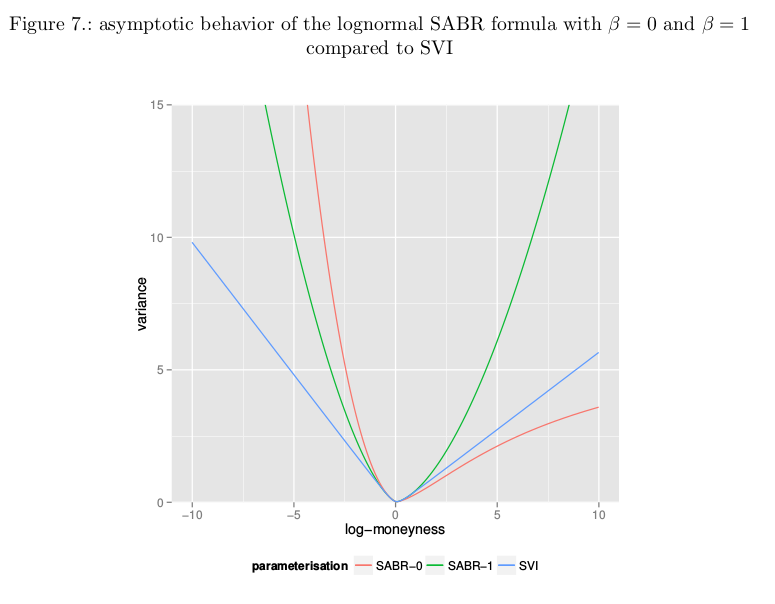
Asymptotic Behavior of SVI vs SABR

Tue, Sep 23, 2014 The variance under SVI becomes linear when the log-moneyness is very large in absolute terms. The lognormal SABR formula with beta=0 or beta=1 has a very different behavior. Of course, the theoretical SABR model has actually a different asymptotic behavior.

As an illustration, we calibrate SABR (with two different values of beta) and SVI against the same implied volatility slice and look at the wings behavior.

While the Lee moments formula implies that the variance should be at most linear, something that the SABR formula does not respect. It is in practice not the problem with SABR as the actual Lee boundary: V(x) < 2|x|/T (where V is the square of the implied volatility and x the log-moneyness) is attained for extremely low strikes only with SABR, except maybe for very long maturities.

A related behavior is the fact that the lognormal SABR formula can actually match steeper curvatures at the money than SVI for given asymptotes.