Andreasen Huge extrapolation
There are not many arbitrage free extrapolation schemes. Benaim et al. extrapolation is one of the few that claims it. However, despite the paper’s title, it is not truely arbitrage free. The density might be positive, but the forward is not preserved by the implied density. It can also lead to wings that don’t obey Lee’s moments condition.
On a Wilmott forum, P. Caspers proposed the following counter-example based on extrapolating SABR: \( \alpha=15%, \beta=80%, \nu=50%, \rho=-48%, f=3%, T=20.0 \). He cut this smile at 2.5% and 6% and used the BDK extrapolation scheme with mu=nu=1.
A truly arbitrage free extrapolation can be obtained through Andreasen Huge volatility interpolation, making sure the grid is wide enough to allow extrapolation. Their method is basically a one step finite difference implicit Euler scheme applied to a local volatility parameterization that has as many parameters than prices. The method is presented with piecewise constant local volatility, but actually used with piecewise linear local volatility in their example.
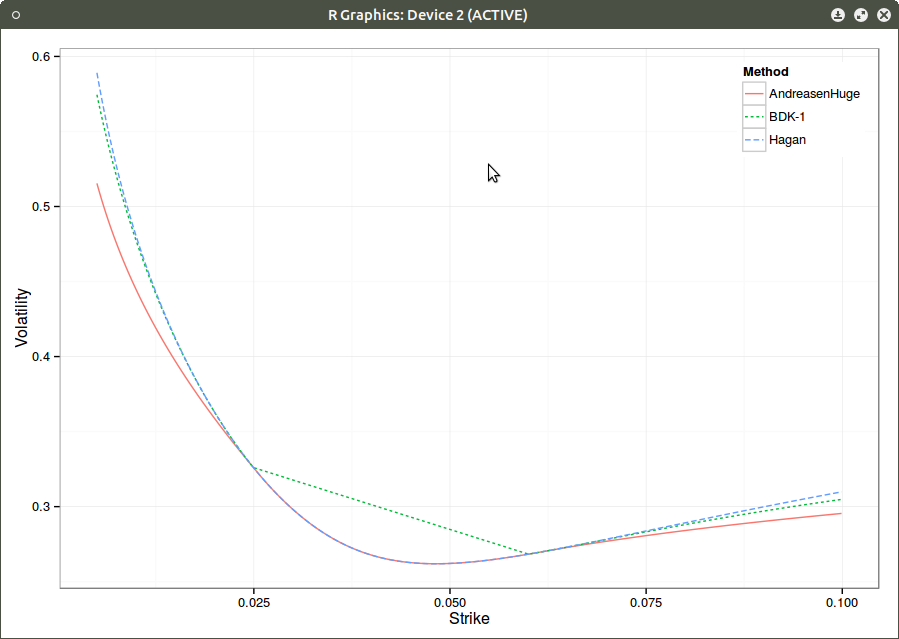
Smile.
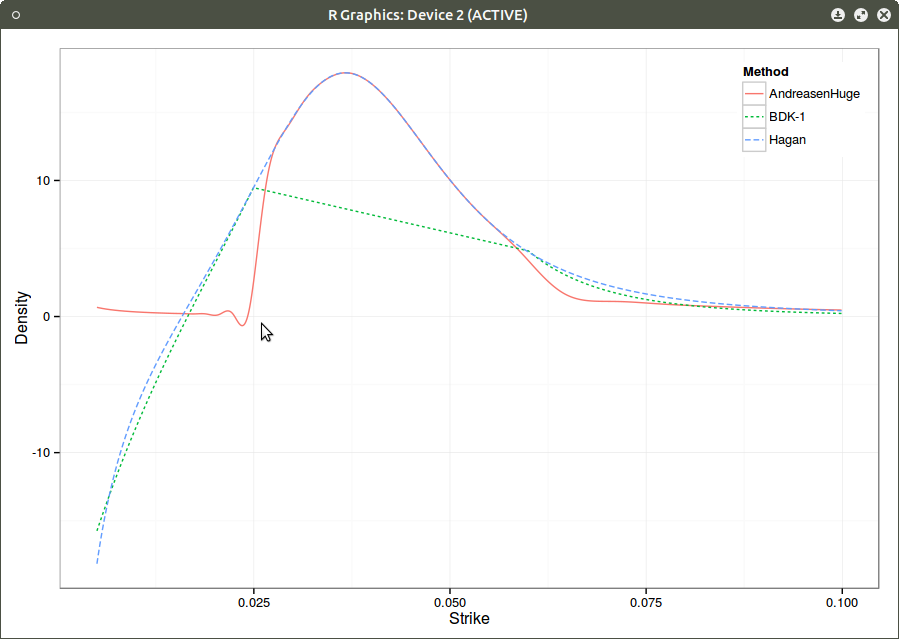
Density with piecewise linear local volatility.
There is still a tiny oscillation that makes the density negative, but one understands why typical extrapolations fail on the example: the change in density must be very steep. Note that moving the left extrapolation point even closer to the forward might fix BDK negative density, but we are already very close, and we can really wonder if going closer is really a good idea since we would effectively use a somewhat arbitrary extrapolation in most of the interpolation zone.
It turns out that we can also use a cubic spline local volatility with linear extrapolation, and the density would look then:
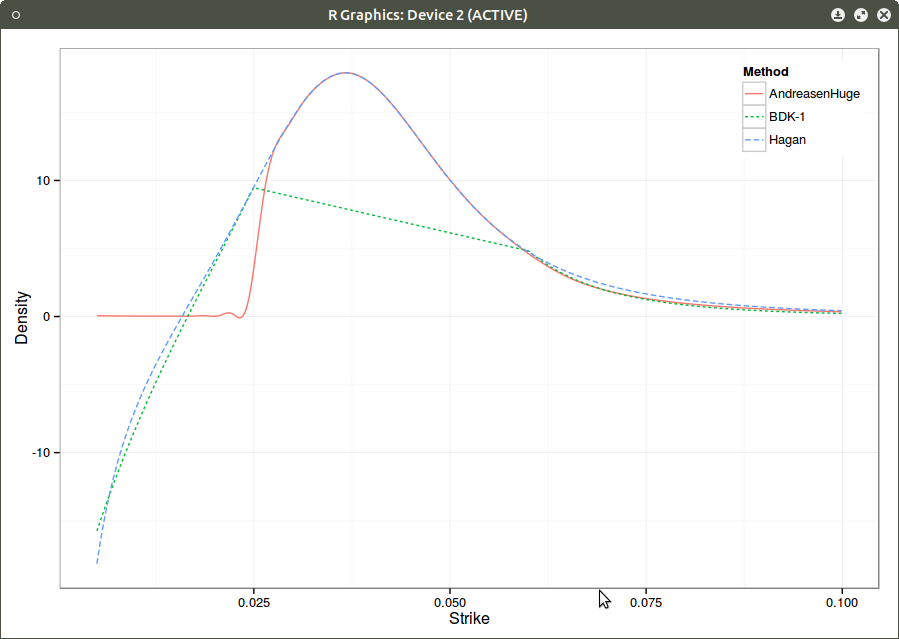
Density with cubic spline local volatility.
Interestingly, the right side of the density is much better captured. The wiggle persists, although it is smaller. This is likely due to the fact that I am using a cubic spline on top of the finite difference prices (in order to have a C2 density). Using a better C2 convexity preserving interpolation would likely remove this artefact.
Those figures also show why relying just on extrapolation to fix SABR is not necessarily a good idea: even a real arbitrage free extrapolation will make a not so meaningful density. The proper solution is to really use Hagan’s arbitrage free SABR PDE, which would be as nearly fast in this case.